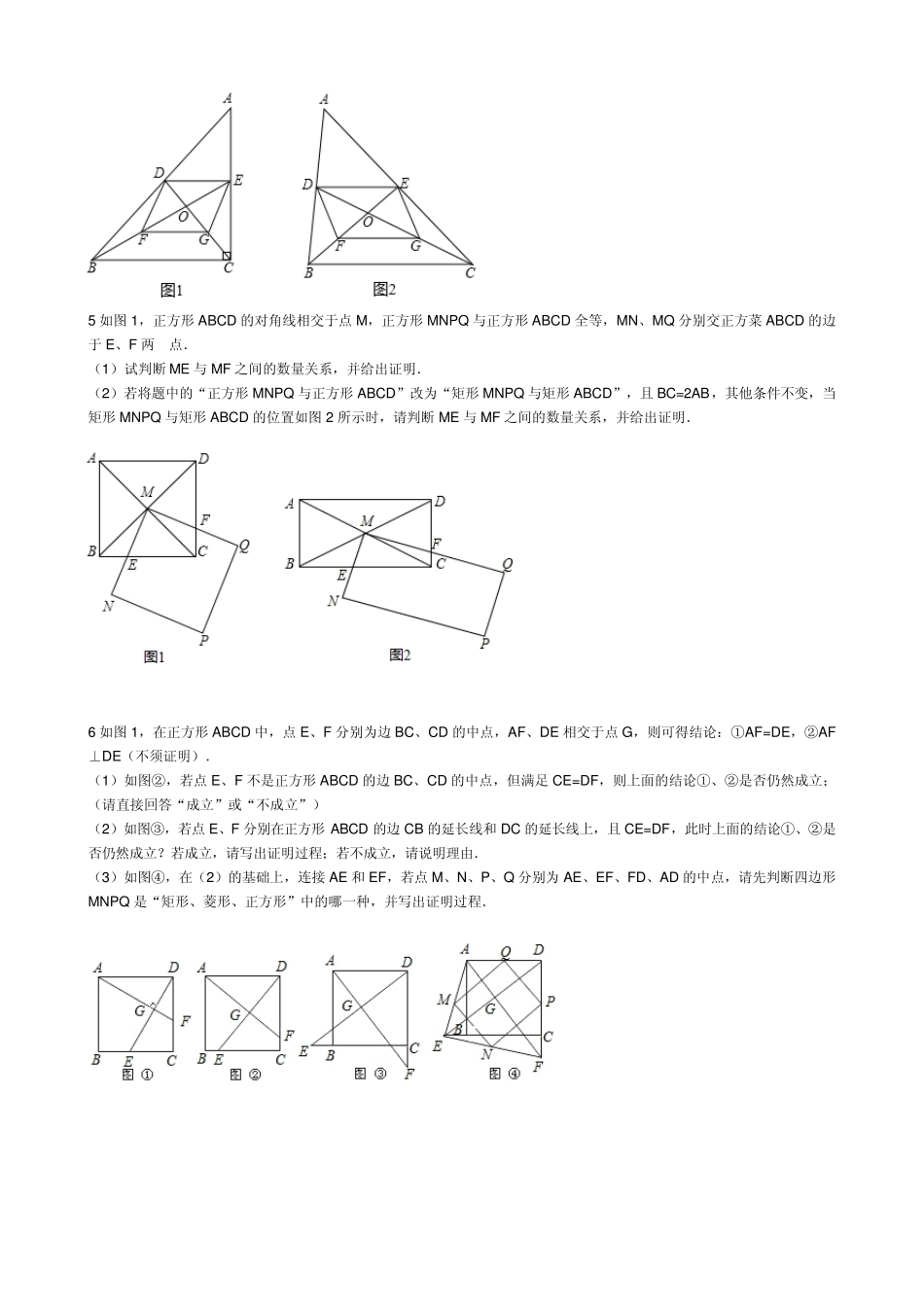
1 .如图,已知E,F,G,H分别是四边形ABCD四边形的中点;(1)当满足条件四边形EFGH是矩形;(2)当满足条件四边形EFGH是菱形;(3)当满足条件四边形EFGH是正方形. 2 已知,如图,四边形ABCD 是菱形,∠B 是锐角,AF⊥BC 于点F,CH⊥AD 于点H,在AB 边上取点E,使得AE=AH,在CD 边上取点G,使得CG=CF,连接EF、FG、GH、HE. (1)求证:四边形EFGH 是矩形; (2)当∠B 为多少度时,四边形EFGH 是正方形?并证明. 3 如图,根据图形解答下列问题 (1)如图,以△ABC 三边向外分别作等边△ACD、△ABE、△BCF,证明四边形ADFE 是平行四边形. (2)△ABC 满足什么条件时,四边形ADFE 是矩形? (3)△ABC 满足什么条件时,四边形ADFE 是菱形? (4)△ABC 满足什么条件时,四边形ADFE 是正方形? 4)如图(1),Rt△ABC 中,∠ACB=90°,中线 BE、CD 相交于点O,点F、G 分别是OB、OC 的中点. (1)求证:四边形DFGE 是平行四边形; (2)如果把 Rt△ABC 变为任意△ABC,如图(2),通过你的观察,第(1)问的结论是否仍然成立(不用证明); (3)在图(2)中,试想:如果拖动点A,通过你的观察和探究,在什么条件下四边形DFGE 是矩形,并给出证明; (4)在第(3)问中,试想:如果拖动点A,是否存在四边形DFGE 是正方形或菱形?如果存在,画出相应的图形(不用证明). 5 如图1,正方形ABCD 的对角线相交于点M,正方形MNPQ 与正方形ABCD 全等,MN、MQ 分别交正方菜ABCD 的边于E、F 两 点. (1)试判断ME 与MF 之间的数量关系,并给出证明. (2)若将题中的“正方形MNPQ 与正方形ABCD”改为“矩形MNPQ 与矩形ABCD”,且 BC=2AB,其他条件不变,当矩形MNPQ 与矩形ABCD 的位置如图2 所示时,请判断ME 与MF 之间的数量关系,并给出证明. 6 如图1,在正方形ABCD 中,点E、F 分别为边BC、CD 的中点,AF、DE 相交于点G,则可得结论:①AF=DE,②AF⊥DE(不须证明). (1)如图②,若点E、F 不是正方形ABCD 的边BC、CD 的中点,但满足 CE=DF,则上面的结论①、②是否仍然成立;(请直接回答“成立”或“不成立”) (2)如图③,若点E、F 分别在正方形ABCD 的边CB 的延长线和 DC 的延长线上,且 CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由. (3)如图④,在(2)的基础上,连接 AE 和 EF,若点M、N、P、Q ...