瞬时变化率导数一曲线上一点处的切线VIP免费

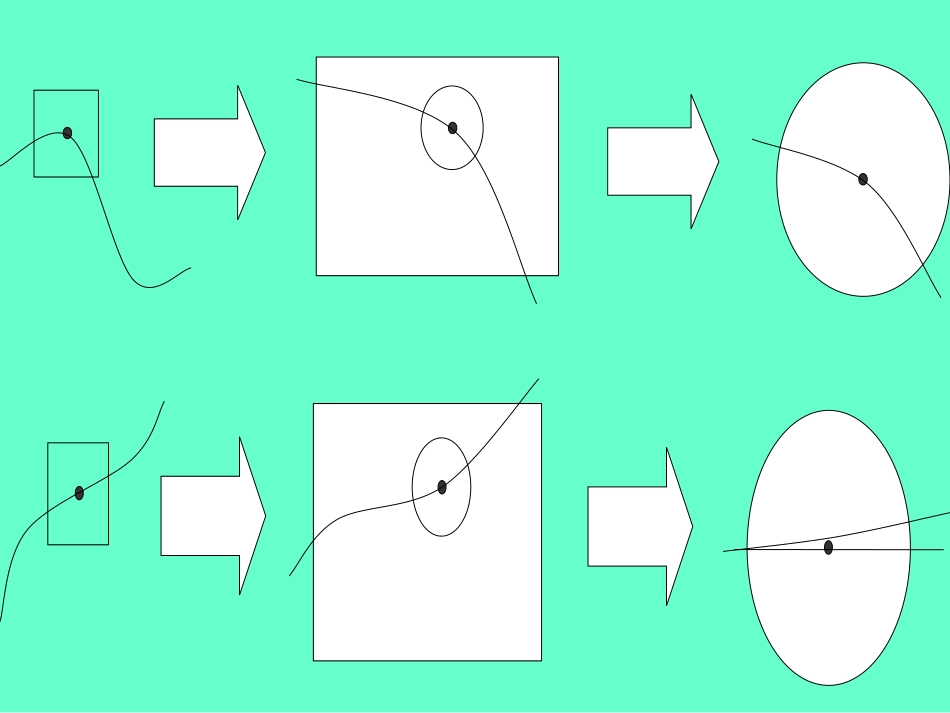
平均变化率)(xf一般的，函数在区间上的平均变化率为],[21xx2121)()(xxxfxf复习放大放大放大放大•1）观察“点P附近的曲线”，随着图形放大，你看到了怎样的现象？•（2）这种现象下，这么一条特殊位置的曲线从其趋势看几乎成了•这种思维方式就叫做“逼近思想”。曲线有点像直线曲线有点像直线直线直线从上面的过程来看：11）．曲线在点）．曲线在点PP附近看上去几乎成了直线附近看上去几乎成了直线22）．继续放大，曲线在点）．继续放大，曲线在点PP附近将逼近一条确定的直线附近将逼近一条确定的直线LL，这条直线是过点，这条直线是过点PP的所有直线中最逼近曲线的一条的所有直线中最逼近曲线的一条直线直线33）．点）．点PP附近可以用这条直线代替曲线附近可以用这条直线代替曲线这样，我们就可以用直线的斜率来刻画曲线经过这样，我们就可以用直线的斜率来刻画曲线经过PP点时上点时上升或下降的“变化趋势”。升或下降的“变化趋势”。PQoxyy=f(x)割线切线l如图，设Q为曲线C上不同于P的一点，直线PQ称为曲线的割线.yOxPQ●P为已知曲线C上的一点，如如何求出点何求出点PP处的切线方程？处的切线方程？●切线定义定义随着点Q沿曲线C向点P运动，直线PQ在点P附近逼近曲线C，当点Q无限逼近点P时，直线PQ最终就成为经过点P处最逼近曲线的直线l，这条直线l也称为曲线在点P处的切线．这种方法叫割线逼近切线.试求f(x)=x2在点(2,4)处的切线斜率．yy·OOPP2244Qxx.442xf(x)4k0x2PQ）处的切线斜率为，在点（从而曲线，无限趋近于常数时，无限趋近于当的斜率则割线设解PQ),)x2(,x2(Q),4,2(P：2试求f(x)=x2在点(2,4)处的切线斜率．x4xxx4x4)x2(k22PQ练习：试求f(x)=x2+1在x=1处的切线斜率．.211xf(x)2k0x2PQ处的切线斜率为在点从而曲线，无限趋近于常数时，无限趋近于当x的斜率则割线设由题意解PQ),1)x1(,x1(Q),2,1(P2，：练习：试求f(x)=x2+1在x=1处的切线斜率．当△△xx无限趋近于无限趋近于00时，时，割线逼近切线，割线斜率逼近切线斜率x2xxx2x2]1)x1[(k22PQ找到定点找到定点PP的坐标的坐标设出动点设出动点QQ的坐的坐标标求出割求出割线斜率线斜率yxOy=f(x)xx0x0+xPQf(x0+x)f(x0)切线割线PP（（xx00,f(x,f(x00))))Q(xQ(x00++△△x,f(xx,f(x00++△△x))x))△△x>0x>0时时,,点点QQ位于点位于点PP的的右侧右侧y=f(x)y=f(x)△△x<0x<0时时,,点点QQ位于点位于点PP的的左侧左侧2.求出割线PQ的斜率,并化简.x)(x)xx(k00PQff求曲线y=f(x)上一点P(x0,f(x0))处切线斜率的一般步骤:3.令Δx趋向于0,若上式中的割线斜率“逼近”一个常数，则其即为所求切线斜率1.设曲线上另一点Q(x0+Δx,f(x0+Δx))MM（即y)变1：已知2()fxx，求曲线()yfx在1x处的切线斜率和切线方程．变2：已知1()fxx，求曲线()yfx在1x处的切线斜率和切线方程．变3：已知2()1fxx，求曲线()yfx在12x处的切线斜率是多少？•例2．已知曲线上一点A(1，2)，求(1)点A处的切线的斜率.(2)点A处的切线方程.22yx课堂练习：练习已知求曲线在处的切线斜率是多少？()fxx12x()yfx练习已知求曲线在处的切线斜率是多少？()fxx12x()yfx小结小结11、曲线上一点、曲线上一点PP处的切线是过点处的切线是过点PP的所有直线中的所有直线中最接近最接近PP点附近曲线的直线，则点附近曲线的直线，则PP点处的变化趋势可点处的变化趋势可以由该点处的切线反映。以由该点处的切线反映。((局部以直代曲局部以直代曲))●22、根据定义、根据定义,,利用割线逼近切线的方法利用割线逼近切线的方法,,可以求可以求出曲线在一点处的切线斜率和方程。出曲线在一点处的切线斜率和方程。割线PQP点处的切线Q无限逼近P时割线PQ的斜率P点处的切线斜率Q无限逼近P时Q无限逼近P时即区间长度趋向于0令横坐标无限接近函数在区间[xP,xQ](或[xQ,xP]）上的平均变化率P点处的瞬时变化率(导数)课后作业1．曲线的方程为y=x2+1，那么求此曲线在点P(1，2)处的切线的斜率，以及切线的方程.2．求曲线f(x)=x3+2x+1在点(1，4)处的切线方程.3．求曲线f(x)=31x3－x2+5在x=1处的切线的倾斜角.4．y=x3在点P处的切线斜率为3，求点P的坐标.5．求下列曲线在指定点处的切线斜率.(1)y=－3x+2,x＝２处奎屯王新敞新疆（２）y＝11x，x＝０处．6..求曲线y=x2+1在点P(－2，5)处的切线方程.