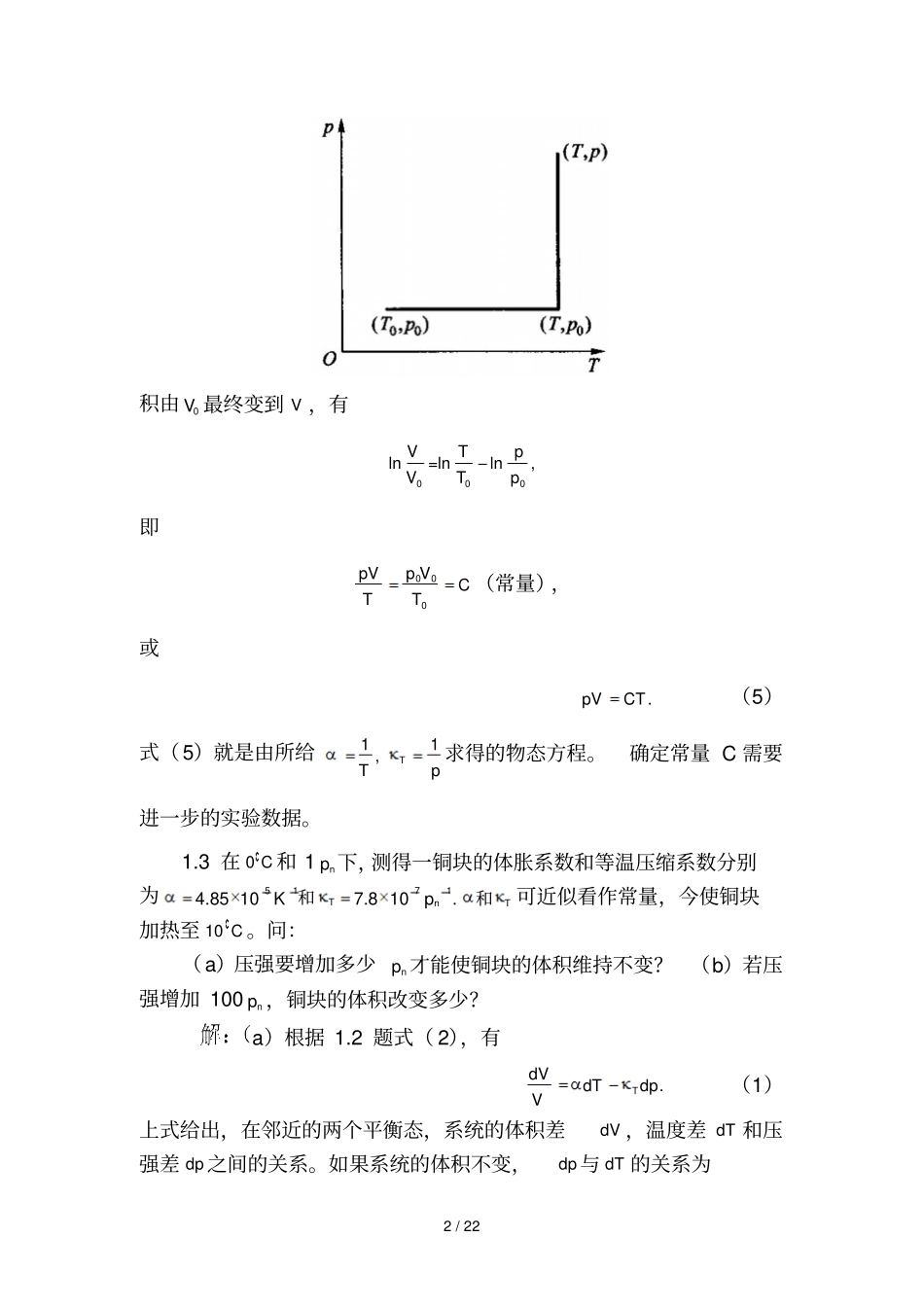
1 / 22 1.2 证明任何一种具有两个独立参量,T p 的物质,其物态方程可由实验测得的体胀系数及等温压缩系数,根据下述积分求得:lnTV =αdTκ dp如果11,TTp ,试求物态方程。解:以,Tp 为自变量,物质的物态方程为,,VV Tp其全微分为.pTVVdVdTdpTp(1)全式除以 V ,有11.pTdVVVdTdpVVTVp根据体胀系数和等温压缩系数T 的定义,可将上式改写为.TdVdTdpV(2)上式是以,Tp 为自变量的完整微分,沿一任意的积分路线积分,有ln.TVdTdp(3)若11,TTp ,式( 3)可表为11ln.VdTdpTp(4)选择图示的积分路线,从00(,)Tp积分到0,Tp,再积分到(,Tp ),相应地体2 / 22 积由0V 最终变到 V ,有000ln=lnln,VTpVTp即000p VpVCTT(常量),或.pVCT(5)式(5)就是由所给11,TTp 求得的物态方程。确定常量 C 需要进一步的实验数据。1.3 在 0 C 和 1np 下,测得一铜块的体胀系数和等温压缩系数分别为51714.85 10K7.8 10.npT和T和可近似看作常量,今使铜块加热至 10 C 。问:(a)压强要增加多少np 才能使铜块的体积维持不变?(b)若压强增加 100np ,铜块的体积改变多少?a)根据 1.2 题式( 2),有.TdVdTdpV(1)上式给出,在邻近的两个平衡态,系统的体积差dV ,温度差 dT 和压强差 dp之间的关系。如果系统的体积不变,dp与 dT 的关系为3 / 22 .TdpdT(2)在和T 可以看作常量的情形下,将式(2)积分可得2121 .TppTT(3)将式(2)积分得到式( 3)首先意味着,经准静态等容过程后,系统在初态和终态的压强差和温度差满足式(3)。 但是应当强调,只要初态1,VT 和终态2,VT是平衡态,两态间的压强差和温度差就满足式(3)。 这是因为,平衡状态的状态参量给定后,状态函数就具有确定值,与系统到达该状态的历史无关。本题讨论的铜块加热的实际过程一般不会是准静态过程。在加热过程中,铜块各处的温度可以不等,铜块与热源可以存在温差等等,但是只要铜块的初态和终态是平衡态,两态的压强和温度差就满足式(3)。将所给数据代入,可得52174.851010622.7.8 10nppp因此,将铜块由0 C 加热到 10 C ,要使铜块体积保持不变,压强要增强 622np(b)1.2 题式( 4)可改写为21211.TVTTppV(4)将所给数据代入,有57144.85 10107.8 101004.07 10 .VV因此,将铜块由 0 C 加热至 10 C ,压强由 1np 增加 100np ,铜块体积将增加原体积的44.0710倍。1.12 假设理想气体的pVCC和之比 是...