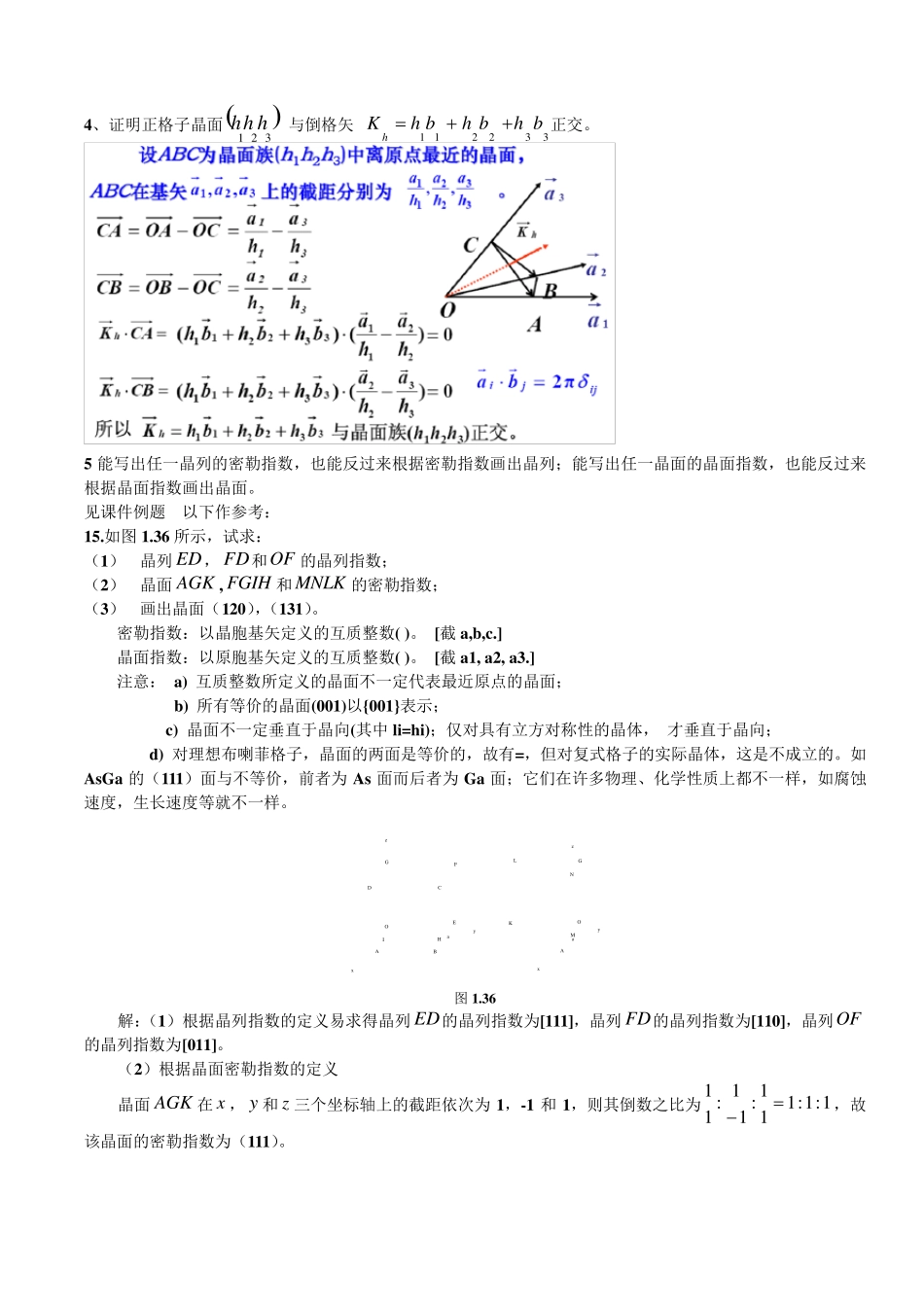
第一章 晶体结构 1、把等体积的硬球堆成下列结构,求球可能占据的最大体积和总体积之比。 (1)简立方 (2)体心立方 (3)面心立方(4)金刚石 解:(1)、简立方,晶胞内含有一个原子 n=1,原子球半径为 R,立方晶格的顶点原子球相切,立方边长 a=2R,体积为32 R , 所以 33344330 .5 262nRRKVR (2)、体心立方晶胞内含有 2 个原子 n=2,原子球半径为 R,晶胞边长为 a,立方晶格的体对角线原子球相切,体对角线长为 4 个原子半径,所以43aR 3334423330 .6 8843nRRKVR (3)、面心立方晶胞内含有 4 个原子 n=4,晶胞的面对角线原子球相切,面对角线长度为 4 个原子半径,立方体边长为 a,所以42aR 3334442330 .7 4642nRRKVR (4)、金刚石在单位晶格中含有 8 个原子,碳原子最近邻长度 2R 为体对角线 14 长,体对角线为 83Ra 3334483330 .3 41 683nRRKVR 2、证明面心立方和体心立方互为倒格子。 09 级微电子学专业《固体物理》期末考复习题目 至诚 学院 信息工程 系 微电子学 专业 姓名: 陈长彬 学号: 210991803 3、证明:倒格子原胞体积为3*2cvv,其中 v c 为正格子原胞的体积。 4、证明正格子晶面 与倒格矢 正交。 5 能写出任一晶列的密勒指数,也能反过来根据密勒指数画出晶列;能写出任一晶面的晶面指数,也能反过来根据晶面指数画出晶面。 见课件例题 以下作参考: 15.如图 1.36 所示,试求: (1) 晶列 ED, FD和OF 的晶列指数; (2) 晶面 AGK , FGIH 和 MNLK 的密勒指数; (3) 画出晶面(120),(131)。 密勒指数:以晶胞基矢定义的互质整数( )。 [截 a,b,c.] 晶面指数:以原胞基矢定义的互质整数( )。 [截 a1, a2, a3.] 注意: a) 互质整数所定义的晶面不一定代表最近原点的晶面; b) 所有等价的晶面(001)以{001}表示; c) 晶面不一定垂直于晶向(其中 li=hi);仅对具有立方对称性的晶体, 才垂直于晶向; d) 对理想布喇菲格子,晶面的两面是等价的,故有=,但对复式格子的实际晶体,这是不成立的。如AsGa 的(111)面与不等价,前者为 As 面而后者为 Ga 面;它们在许多物理、化学性质上都不一样,如腐蚀速度,生长速度等就不一样。 axyzABDCGFEOIHyxAaKOGLNMz 图 1.3...