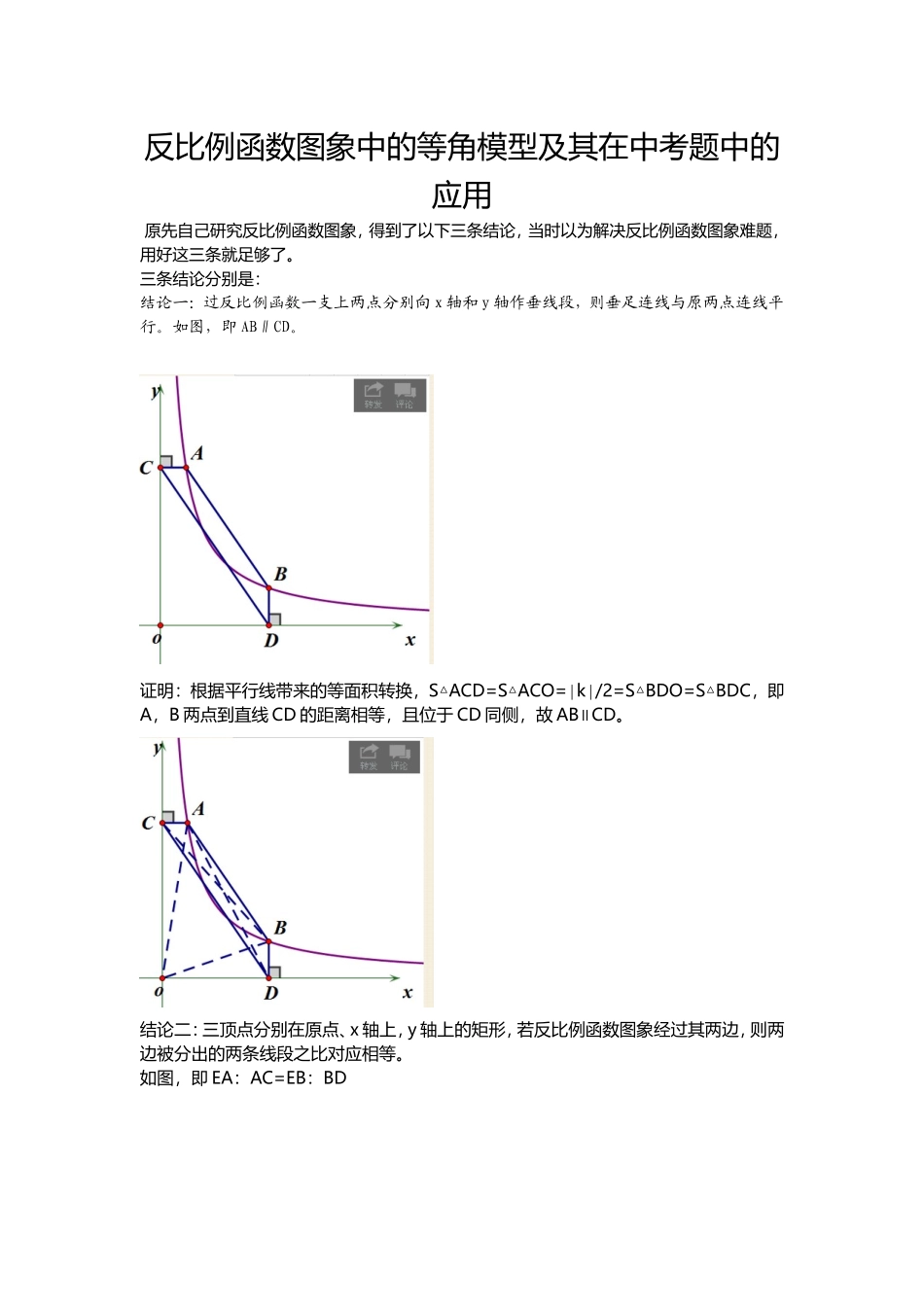
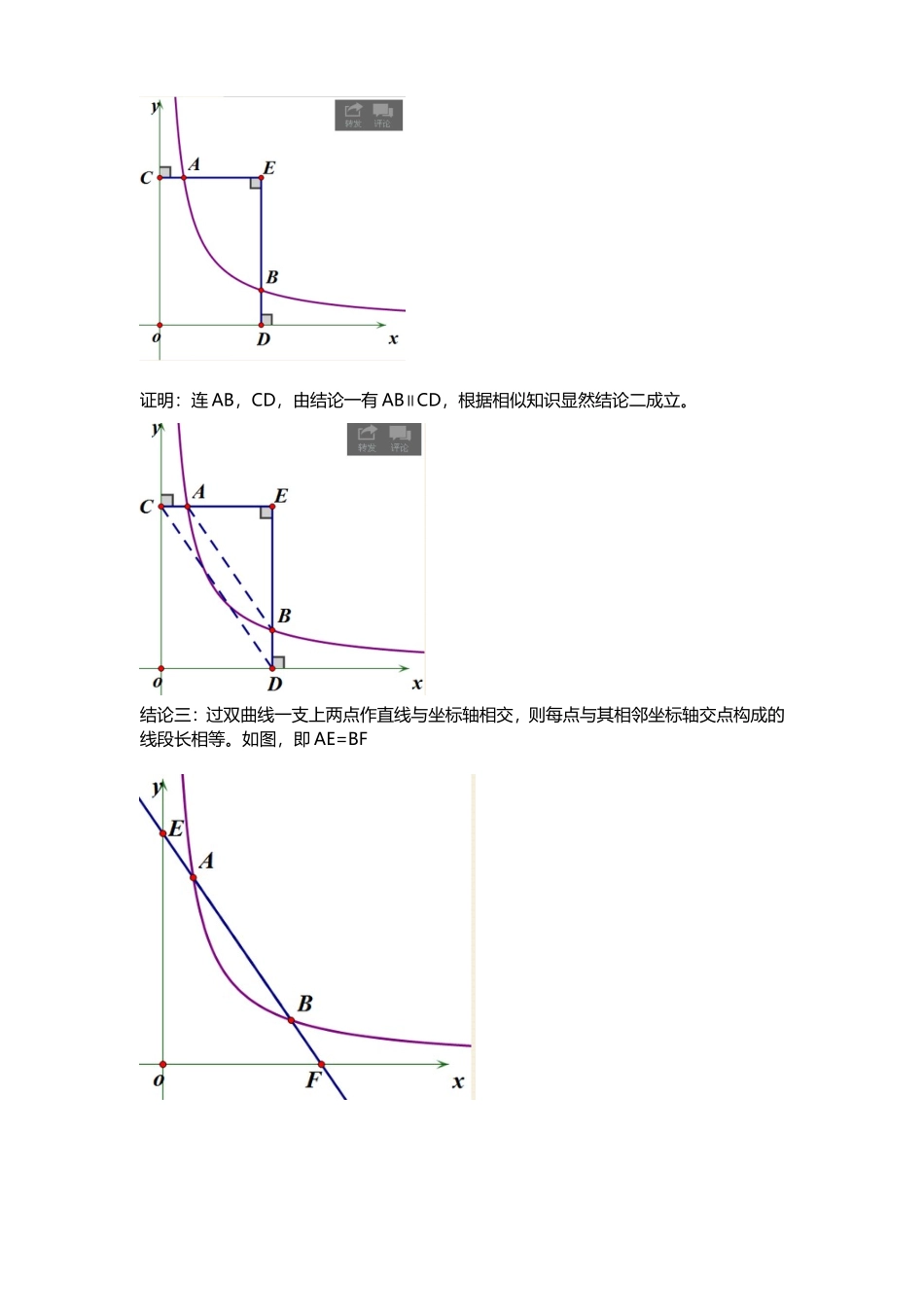
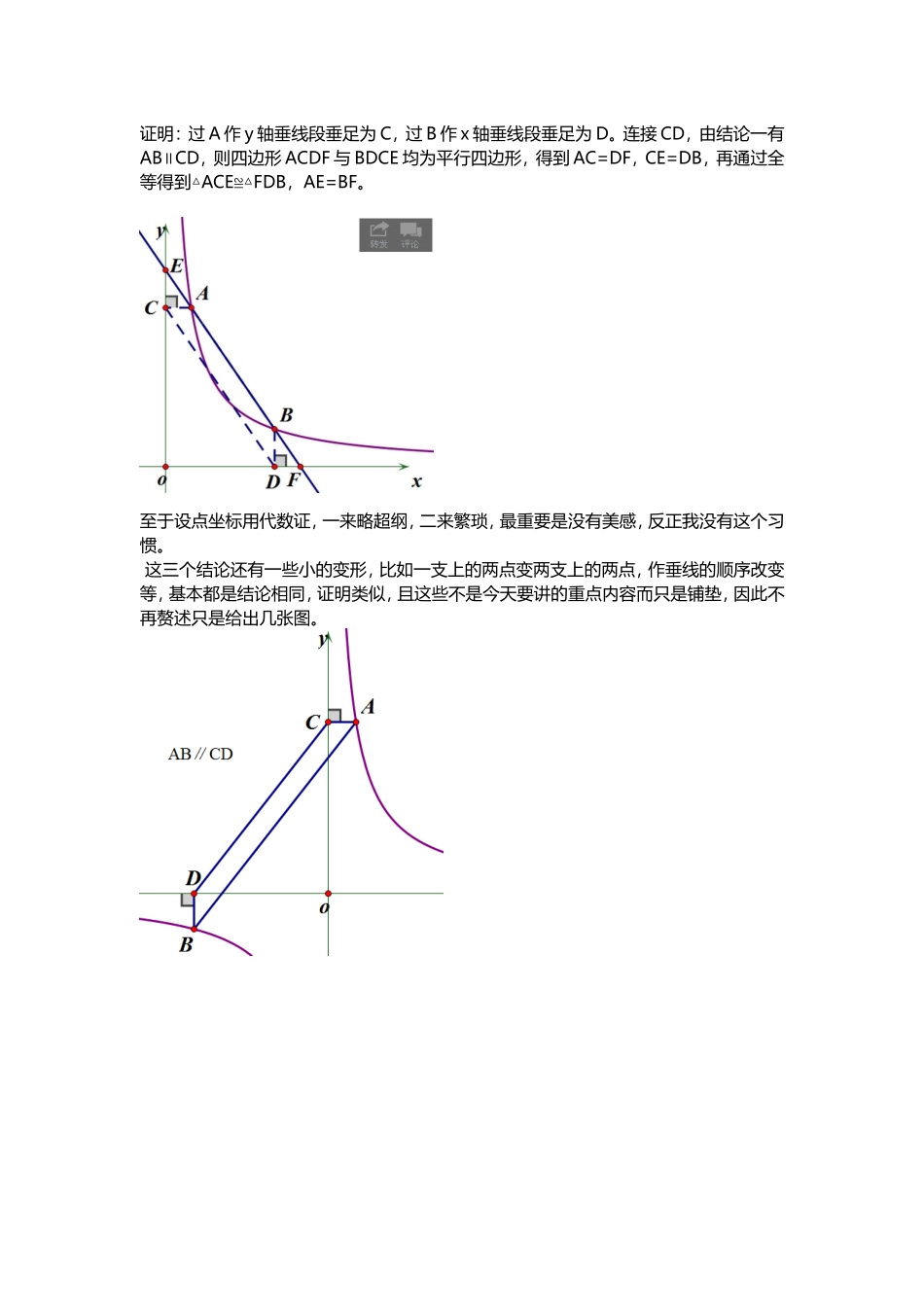
反比例函数图象中的等角模型及其在中考题中的应用 原先自己研究反比例函数图象,得到了以下三条结论,当时以为解决反比例函数图象难题,用好这三条就足够了。三条结论分别是:结论一:过反比例函数一支上两点分别向 x 轴和 y 轴作垂线段,则垂足连线与原两点连线平行。如图,即 AB∥CD。证明:根据平行线带来的等面积转换,S△ACD=S△ACO=∣k∣/2=S△BDO=S△BDC,即A,B 两点到直线 CD 的距离相等,且位于 CD 同侧,故 AB∥CD。结论二:三顶点分别在原点、x 轴上,y 轴上的矩形,若反比例函数图象经过其两边,则两边被分出的两条线段之比对应相等。 如图,即 EA:AC=EB:BD证明:连 AB,CD,由结论一有 AB∥CD,根据相似知识显然结论二成立。结论三:过双曲线一支上两点作直线与坐标轴相交,则每点与其相邻坐标轴交点构成的线段长相等。如图,即 AE=BF证明:过 A 作 y 轴垂线段垂足为 C,过 B 作 x 轴垂线段垂足为 D。连接 CD,由结论一有AB∥CD,则四边形 ACDF 与 BDCE 均为平行四边形,得到 AC=DF,CE=DB,再通过全等得到△ACE≌△FDB,AE=BF。至于设点坐标用代数证,一来略超纲,二来繁琐,最重要是没有美感,反正我没有这个习惯。 这三个结论还有一些小的变形,比如一支上的两点变两支上的两点,作垂线的顺序改变等,基本都是结论相同,证明类似,且这些不是今天要讲的重点内容而只是铺垫,因此不再赘述只是给出几张图。今天要讲的内容:后来才发现, 反比例函数图象还有一些模型和结论,不能由前三个结论直接解决,但可以以前三个结论为基础推出结果间接解决。有如下结论(个人称为等角模型):结论四:双曲线一支上任取两点 A,B,在围着双曲线该支所在象限的坐标轴上再取两点C,D,使 ABCD 构成平行四边形。则有:∠DCO=∠BCx,∠CDO=∠ADy证明:过 A 向 y 轴作垂线段垂足 E,过 B 向 x 轴作垂线段垂足 F,连接 EF。由结论一,有EF∥CD,则 CO:OD=CF:ED。由全等知△AED≌△CFB,ED=BF,即有 CO:OD=CF:BF,△COD∽△CFB,∠DCO=∠BCx,∠CDO=∠ADy。结论五:双曲线一支上任取两点 A,B,在在围着双曲线该支所在象限对顶的象限的坐标轴上再取两点 C,D,使 ABCD 构成平行四边形。则有:∠ADO=∠CDO,∠BCO=∠DCO,若 AD 交 y 轴于 F,BC 交 x 轴于 E,则四边形 CDFE 为菱形。证明:过 A 作 x 轴平行线,过 D 作 y 轴平行线,两者交于 G,AG 交 y 轴于 ...