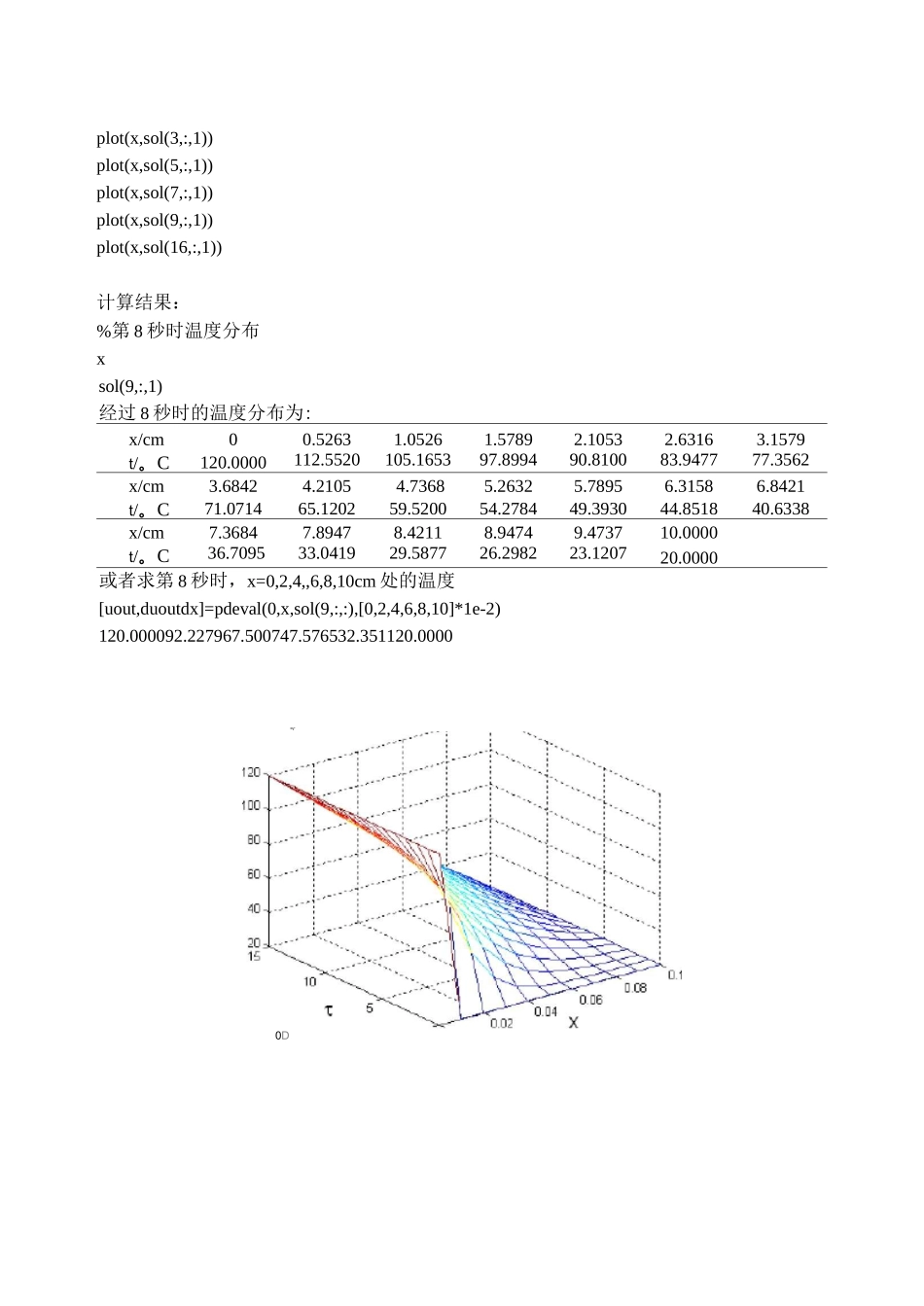
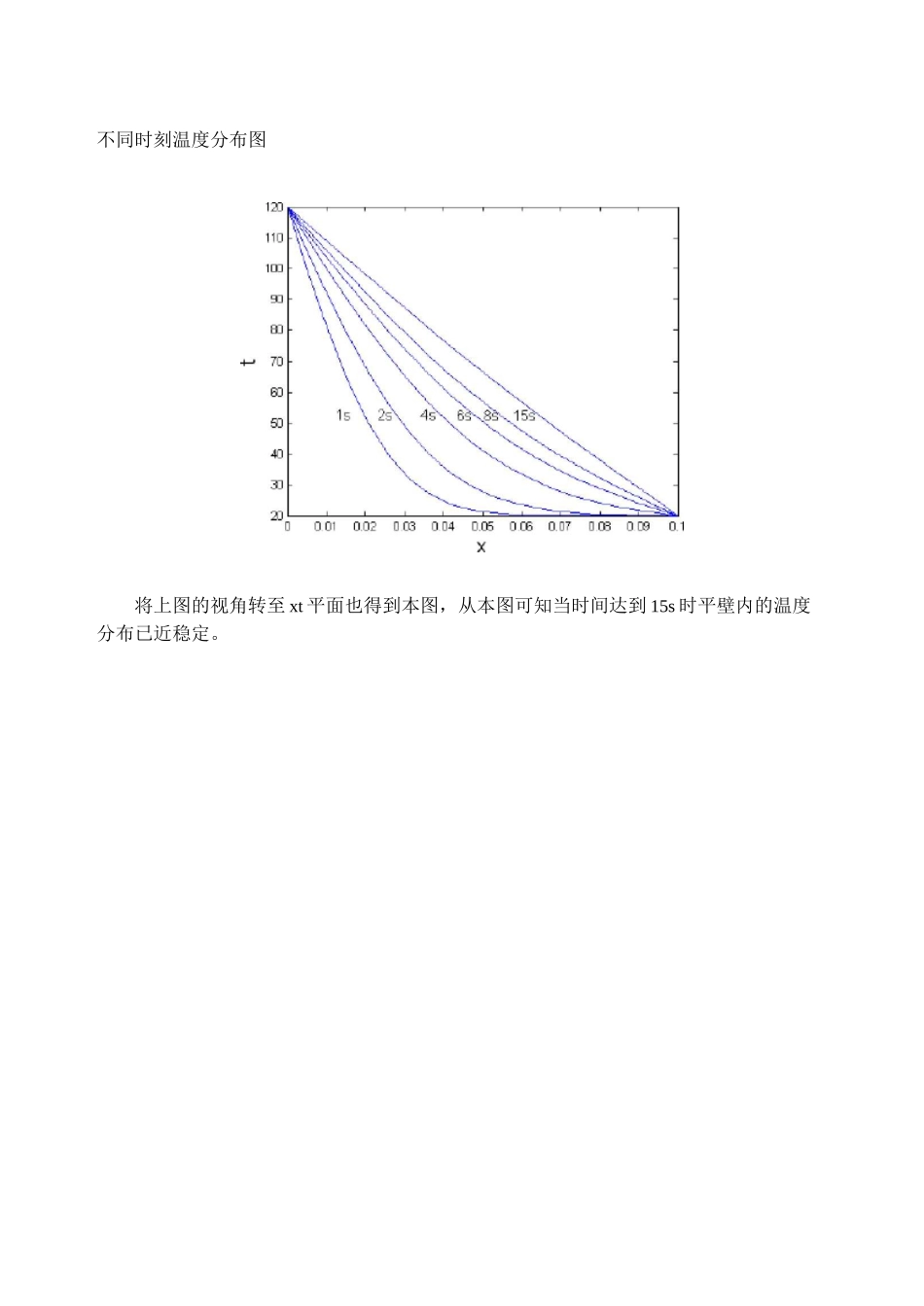
偏微分方程组解法某厚度为 10cm 平壁原温度为 20。C,现其两侧面分别维持在 20。C 和 120。C,试求经过 8 秒后平壁内温度分布,并分析温度分布随时间的变化直至温度分布稳定为止。dtd21=a氏 dx2式中 a 为导温系数,cm2/s;a=2。解:模型转化为标准形式:1dt=d21adTdx2初始条件为:t(x,0)=20边界条件为:t(0,T)=120,t(0.1,T)=20函数:pdefun.m%偏微分方程(一维动态传热)function[c,f,s]=pdefun(x,t,u,dudx)c=1/2e-4;f=dudx;s=0;icbun.m%偏微分方程初始条件(一维动态传热)functionu0=icbun(x)u0=20;bcfun.m%偏微分方程边界条件(一维动态传热)function[pl,ql,pr,qr]=bcfun(xl,ul,xr,ur,t)pl=ul-120;ql=0;pr=ur-20;qr=0;命令:x=linspace(0,10,20)*1e-2;t=linspace(0,15,16);sol=pdepe(0,@pdefun,@icfun,@bcfun,x,t);mesh(x,t,sol(:,:,1))%温度与时间和空间位置的关系图%画 1、2、4、6、8、15s 时刻温度分布图plot(x,sol(2,:,l))Is 时刻,(因为本题 sol 第一行为 0 时亥 0)holdonplot(x,sol(3,:,1))plot(x,sol(5,:,1))plot(x,sol(7,:,1))plot(x,sol(9,:,1))plot(x,sol(16,:,1))计算结果:%第 8 秒时温度分布xsol(9,:,1)经过 8 秒时的温度分布为:x/cm00.52631.05261.57892.10532.63163.1579t/。C120.0000112.5520105.165397.899490.810083.947777.3562x/cm3.68424.21054.73685.26325.78956.31586.8421t/。C71.071465.120259.520054.278449.393044.851840.6338x/cm7.36847.89478.42118.94749.473710.0000t/。C36.709533.041929.587726.298223.120720.0000或者求第 8 秒时,x=0,2,4,,6,8,10cm 处的温度[uout,duoutdx]=pdeval(0,x,sol(9,:,:),[0,2,4,6,8,10]*1e-2)120.000092.227967.500747.576532.351120.0000=r-0D不同时刻温度分布图将上图的视角转至 xt 平面也得到本图,从本图可知当时间达到 15s 时平壁内的温度分布已近稳定。某厚度为 20cm 钢板原温度为 20。C,现将其置于 1000。C 的炉中加热,平壁导热系数为 34.8W/m・。C,对流传热系数 h=174W/m2・。C,导温系数为 a=0.555x10-5m2/s;试分析温度分布随时间的变化及钢板表面温度达到 500。C 时所需的时间。dtd21=a氏 dx2解:模型转化为标准形式:1dt_d21adTdx2初始条件为:t(x,0)_20边界条件为:)()dt(0,T)_0(平壁中心坐标为 0,绝热),hit(0.1,T)-1]_-Xdt(0-1,T)dx8dx函数:pdefun1.m%偏微分方程(一维动态平壁两侧对流)function[c,f,s]=pdefun1(x,t,u,d...