由弯矩引起的正应力VIP免费

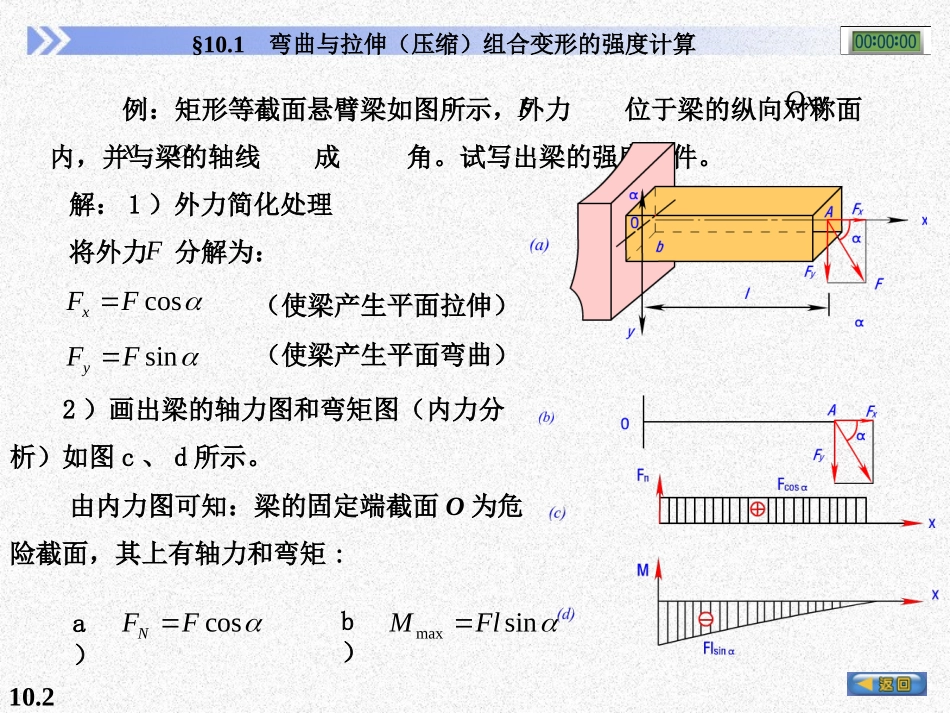
10.1第10章组合变形时杆件的强度计算§10.1弯曲与拉伸（压缩）组合变形的强度计算§10.2弯曲与扭转组合变形的强度计算小结10.2§10.1弯曲与拉伸（压缩）组合变形的强度计算例：矩形等截面悬臂梁如图所示，外力位于梁的纵向对称面内，并与梁的轴线成角。试写出梁的强度条件。FOxyx解：1）外力简化处理将外力分解为：FcosFFxsinFFy（使梁产生平面拉伸）（使梁产生平面弯曲）2）画出梁的轴力图和弯矩图（内力分析）如图c、d所示。由内力图可知：梁的固定端截面O为危险截面，其上有轴力和弯矩:a）cosFFNb）sinmaxFlM10.3§10.1弯曲与拉伸（压缩）组合变形的强度计算3）应力分析：AFAFNNcos(a)由轴力引起的正应力：(b)由弯矩引起的正应力：ZZMWFlWMsinmax(c)两种俱为正应力，可以叠加。（如图10.3e所示）截面O的上、下边缘各点为危险点，且均处于单向应力状态。（如图f所示）从图10.3e可以看出，最大拉应力发生在O截面的上边缘；当发生弯、压组合变形时，从图10.3e可以看出，最大拉应力发生在O截面的下边缘。强度条件可写成统一的表达式为：AFWMNZMAXmax10.4§10.1弯曲与拉伸（压缩）组合变形的强度计算例10.1简易悬臂吊车如图10.4a所示，起吊重力，，kN15F横梁为工字钢，30ABNo.25aMPa100,试校核该梁的强度。CF解：1）外力简化：先求支反力，由0)(FMA即02sin4CFF得：kN601544sin2FFFC将分解为：kN52cosCxCFFkN30sinCyCFF并由，求得：0xF0yF，kN52xCxAFFkN15yAF可以看出梁承受弯曲与压缩组合变形。10.5§10.1弯曲与拉伸（压缩）组合变形的强度计算2）内力分析，画出梁的内力图如图10.4c、d所示。由内力图可看出截面C左侧为危险面。其应力分布如图10.4e所示。由式（10.1）可得：a25.No3）校核强度：由附录型钢表查得工字钢23cm54.48cm402AWZAFWMNZmaxmax43631054.481052104021030MPa2.85Pa103.856==强度足够。10.6§10.1弯曲与拉伸（压缩）组合变形的强度计算例10.2夹具的受力和尺寸如图所示。已知，kN2Fmm22mm10mm60h,b,e，材料的许用应力,MPa170σ试校核夹具竖杆的强度。解：力与竖杆轴线平行，但它不通过竖杆的轴线，竖杆的这种变形通常称为偏心拉伸（或压缩）。F1)计算竖杆所受外力将力向竖杆轴线平移，可得轴向拉力和一作用于纵向对称面内的力偶，FFeMmN120106010233FeMe10.7§10.1弯曲与拉伸（压缩）组合变形的强度计算一对轴向拉力使竖杆轴向拉伸，一对力偶使竖杆发生弯曲变形，所以偏心拉伸（或压缩）实际是弯曲与拉伸（或压缩）的组合变形，称为偏心矩。eMe，2)内力分析kN2FFNmN120eMM3)校核强度竖杆横截面上的最大拉应力发生在右侧边缘各点，其值为：σWMAFσNMPa9.157Pa109.157)022.0(01.061120022.001.0102623max故竖杆强度足够。10.8§10.2弯曲与扭转组合变形的强度计算机械传动中的转轴，一般都是在弯曲与扭转组合变形的情况下工作，如图所示的电动机的转轴等。现对弯曲与扭转组合变形的转轴进行应力分析。画出圆轴的弯矩图和扭矩图如图b、c所示，由图可以看出端面为轴的危险截面，在危险截面上必然存在有弯曲正应力和扭转切应力，根据应力分布情况可知端面的C、D两点为危险点，如图d所示。取原始单元体如图e、f，其应力状态为平面应力状态。且有：AA。PZWTWM,10.9§10.2弯曲与扭转组合变形的强度计算一般轴由塑性材料制成，故由第三、四强度理论建立强度条件：2234r2243r将的表达式代入，并利用圆杆，得到圆轴弯、扭组合变形的强度条件分别为:,ZPWW2ZrWTM223ZrWTM22475.0(10.3)(10.2)10.10例10.3图10.7所示传动轴由电动机带动，轴长，在跨中央安装一胶带轮，重力，半径，胶带紧边张力，松边张力。轴的直径，材料的许用应力为。试按第三强度理论校核该轴的强度。将作用在胶带上的拉力分别向轴线平移，结果如图10.7（b）所示，图中，此力使轴在竖...