奥本海姆《信号与系统(第二版)》习题参考答案

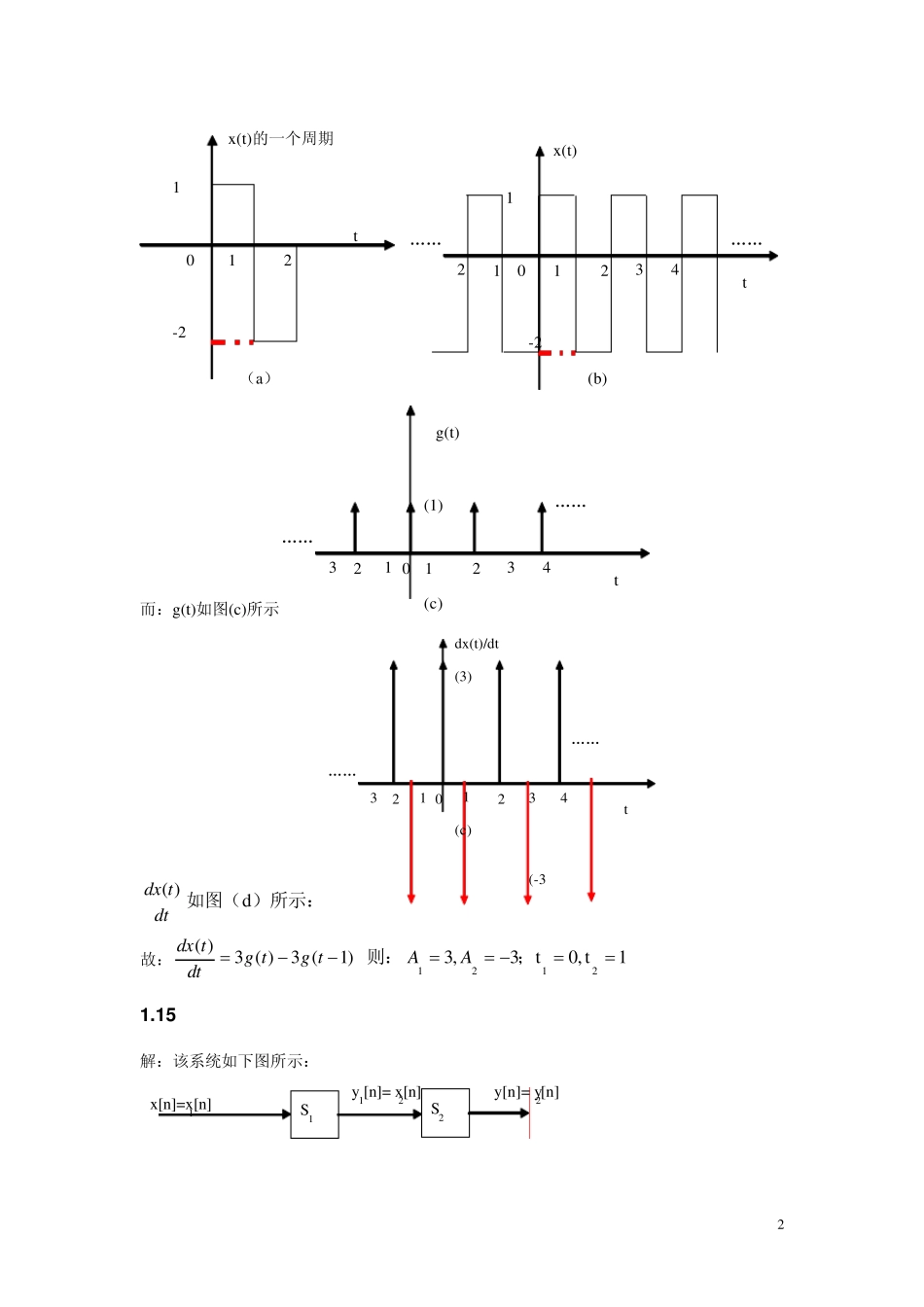
1 第一章作业解答 1 .9 解：（b）jtttjeeetx)1(2)( 由于)()(2)1()1())(1(2txeeeTtxTjtjTtj，故不是周期信号； （或者：由于该函数的包络随t 增长衰减的指数信号，故其不是周期信号；） （c）njenx73][ 则70  7220是有理数，故其周期为N=2； 1 .1 2 解：]4[1][1)1(]1[1][43numnmkknnxmk -3 –2 –1 0 1 2 3 4 5 6 n 1 … … 减去： -3 –2 –1 0 1 2 3 4 5 6 n u [n-4] … 等于： -3 –2 –1 0 1 2 3 4 5 6 n … 故：]3[nu即：M=-1，n0=-3。 1 .1 4 解：x (t)的一个周期如图(a)所示，x (t)如图(b)所示： 2 t x (t)的一个周期 1 -2 0 1 2 （a） t x (t) 1 -2 0 1 2 4 2 1 3 …… …… (b) 而：g(t)如图(c)所示 t g(t) (1) 0 1 2 4 3 2 3 …… …… (c) 1 dttdx)(如图（d）所示： t dx (t)/dt (3) 0 1 2 4 3 2 3 …… …… (c) 1 (-3 故：)1(3)(3)(tgtgdttdx 则：1t,0t3,32121；AA 1 .1 5 解：该系统如下图所示： S1 S2 x [n]=x1[n] y [n]= y2[n] y 1[n]= x2[n] 3 （1）]4[2]3[5]2[2]}4[4]3[2{21]}3[4]2[2{]3[21]2[][][1111111222nxnxnxnxnxnxnxnxnxnyny 即：]4[2]3[5]2[2][nxnxnxny （2）若系统级联顺序改变，该系统不会改变，因为该系统是线性时不变系统。（也可以通过改变顺序求取输入、输出关系，与前面做对比）。 1 .1 7 解：（a）因果性：)(sin)(txty 举一反例：当)0()y(,0intsxt则时输出与以后的输入有关，不是因果的； （b）线性：按照线性的证明过程（这里略），该系统是线性的。 1 .2 0 解：（a）)(21)2cos()(221tjtjeettx 则：)(21)}(21{)(33221tjtjtjtjeeeeTty； (b) tjjtjjtjtjeeeeeettx2121)12()12(22121)(21))21(2cos()( 则：)31(3cos)(212121)()31(3)31(331312teeeeeetytjtjtjjtjj （注意：此系统不是时不变系统。） 1 .2 1 (b)x(2-t) 4 -3 -2 -1 0 1 2 t -4 x (t+2) -1 1 2 3 4 1 2 t 0 x (-t+2) -1 （c）x (2t+1) -2 -1 0 1 1 2 t -3 x (t+1) -1 -1 -0.5 0 0....