军考数学复习提纲VIP免费

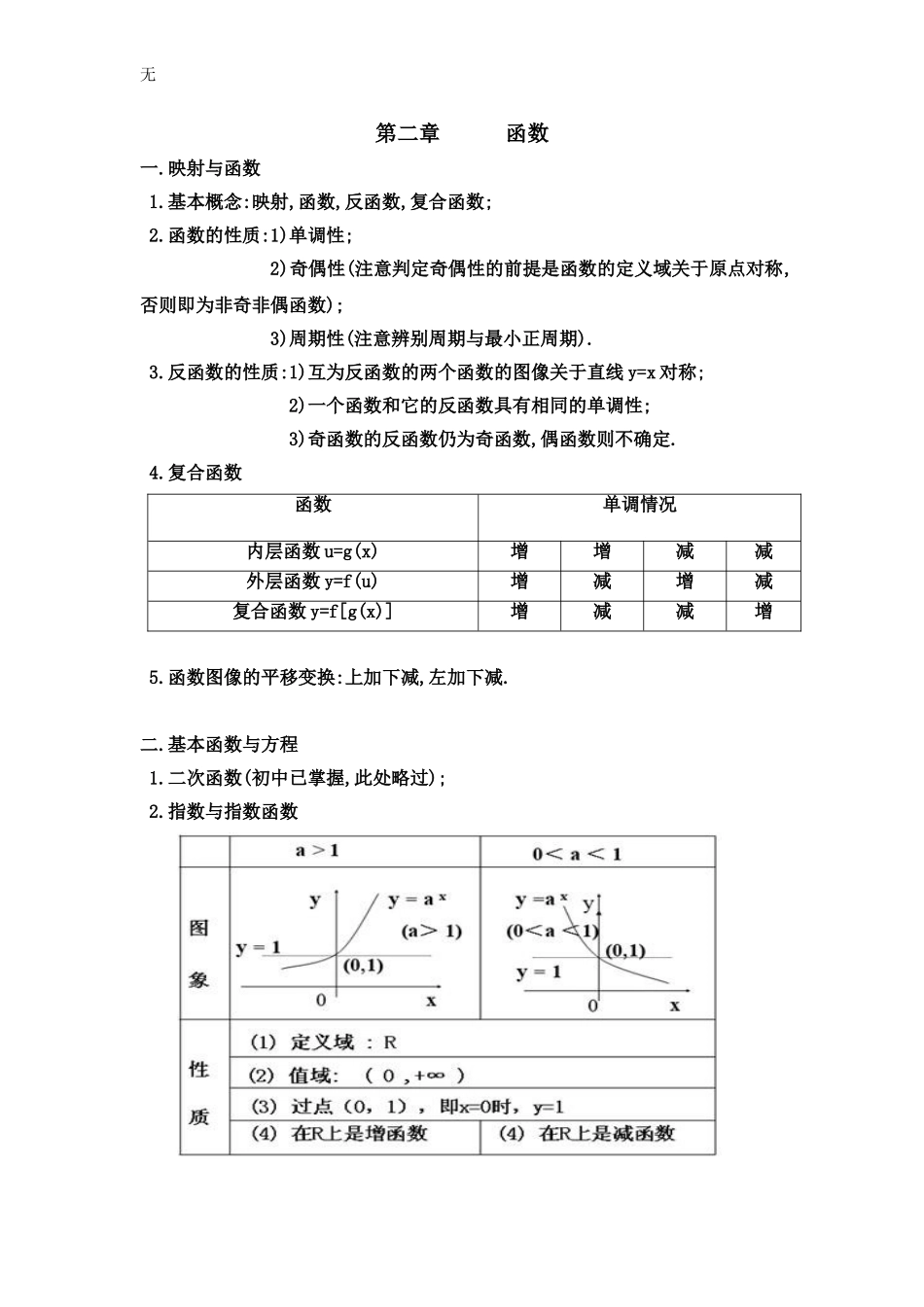
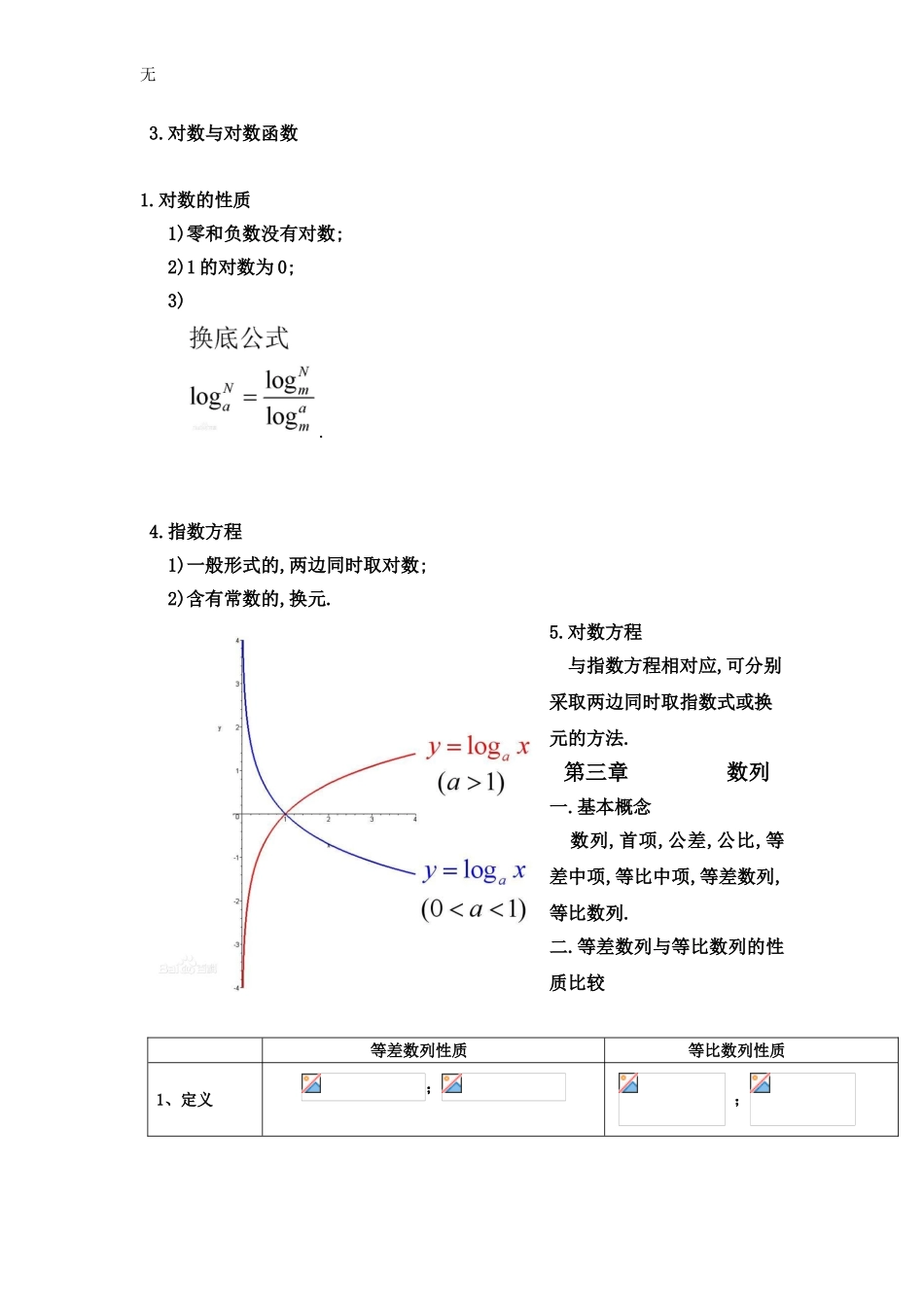
无数学复习提纲第一章集合与简易逻辑一.基本概念1.集合,子集;2.集合的运算:交集,并集,补集;3.逻辑连结词:或,且,非;4.四种命题及其相互关系:原命题,逆命题,否命题,逆否命题;5.充分条件,必要条件,充要条件.无第二章函数一.映射与函数1.基本概念:映射,函数,反函数,复合函数;2.函数的性质:1)单调性;2)奇偶性(注意判定奇偶性的前提是函数的定义域关于原点对称,否则即为非奇非偶函数);3)周期性(注意辨别周期与最小正周期).3.反函数的性质:1)互为反函数的两个函数的图像关于直线y=x对称;2)一个函数和它的反函数具有相同的单调性;3)奇函数的反函数仍为奇函数,偶函数则不确定.4.复合函数函数单调情况内层函数u=g(x)增增减减外层函数y=f(u)增减增减复合函数y=f[g(x)]增减减增5.函数图像的平移变换:上加下减,左加下减.二.基本函数与方程1.二次函数(初中已掌握,此处略过);2.指数与指数函数无3.对数与对数函数1.对数的性质1)零和负数没有对数;2)1的对数为0;3).4.指数方程1)一般形式的,两边同时取对数;2)含有常数的,换元.5.对数方程与指数方程相对应,可分别采取两边同时取指数式或换元的方法.第三章数列一.基本概念数列,首项,公差,公比,等差中项,等比中项,等差数列,等比数列.二.等差数列与等比数列的性质比较等差数列性质等比数列性质1、定义；；无等差数列性质等比数列性质2、通项公式3、前n项和4、中项a、A、b成等差数列A=；是其前k项与后k项的等差中项，即：=a、A、b成等比数列（不等价于，只能）;是其前k项与后k项的等比中项，即：5、下标和公式若m+n=p+q,则特别地,若m+n=2p,则若m+n=p+q,则特别地,若m+n=2p,则6、首尾项性质等差数列的第k项与倒数第k项的和等于首尾两项的和,即：等比数列的第k项与倒数第k项的积等于首尾两项的积,即：7、结论{}为等差数列,若m,n,p成等差数列,则成等差数列{}为等比数列,若m,n,p成等差数列,则成等比数列（两个等差数列的和仍是等差数列）等差数列{},{}的公差分别为,则数列{}仍为等差数列，公差为（两个等比数列的积仍是等比数列）等比数列{},{}的公比分别为,则数列{}仍为等比数列，公差为取出等差数列的所有奇（偶）数项，组成的新数列仍为等差数列，且公差为取出等比数列的所有奇（偶）数项，组成的新数列仍为等比数列，且公比为无等差数列性质等比数列性质若则无此性质；若则无此性质；若无此性质；成等差数列，公差为成等差数列，公比为三.Sn与an的关系an=Sn-(Sn-1);a1=S1.四.错位相减法错位相减法是一种常用的数列求和方法，应用于等比数列与等差数列相乘的形式。形如An=Bn*Cn，其中Bn为等差数列，Cn为等比数列；分别列出Sn，再把所有式子同时乘以等比数列的公比，即kSn；然后错一位，两式相减即可。第六章三角函数一.基本知识弧度制,诱导公式,常用角的三角函数值二.两角和与差的三角函数(必须牢记)1.两角和与差的公式cos(α+β)=cosαcosβ-sinαsinβ;无cos(α-β)=cosαcosβ+sinαsinβ;sin(α+β)=sinαcosβ+cosαsinβ;sin(α-β)=sinαcosβ-cosαsinβ;tan(α+β)=(tanα+tanβ)/(1-tanαtanβ);tan(α-β)=(tanα-tanβ)/(1+tanαtanβ.2.二倍角公式3.半角公式4.三角函数的图像和性质定义域RR值域R周期性奇偶性奇函数偶函数奇函数无单调性上为增函数；上为减函数（）；上为增函数上为减函数（）上为增函数（）1-1y=sinx-32-52-727252322-2-4-3-2432-oyx1-1y=cosx-32-52-727252322-2-4-3-2432-oyx无y=tanx322-32--2oyx第七章向量无一.基本概念向量,向量的模.零向量,平行向量,法向量.二.向量的运算1.向量的加减法(平行四边形定则或三角形法则);2.实数与向量的积设λ、μ是实数，那么满足如下运算性质：(λμ)a=λ(μa);(λ+μ)a=λa+μa;λ(a±b)=λa±λb;(－λ)a=－(λa)=λ(－a).3.向量的数量积1)数量积a·b的几何意义是：a的长度|a|与b在a的方向上的投影|b|cosθ的乘积;2)数量积具有以下性质：a·a=|a|2≥0;a·b=b·a;k(a·b)=(ka)b=a(kb);a·(b+c)=a·b+a·c.4.平面向量1)平面向量基本定理如果是一个平面内的两个不共线向量，那么对这一平面内的任一向量，有且只...