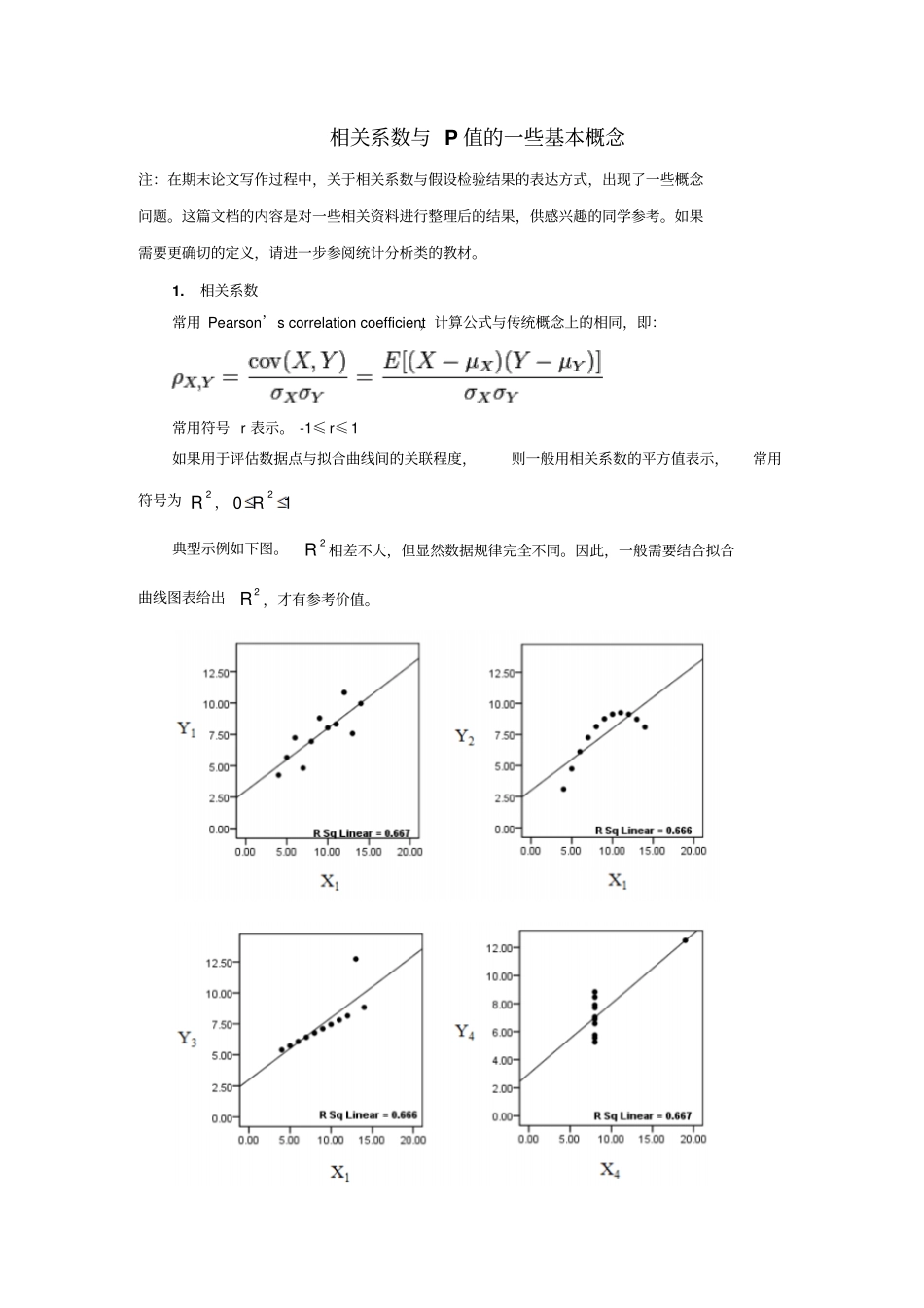
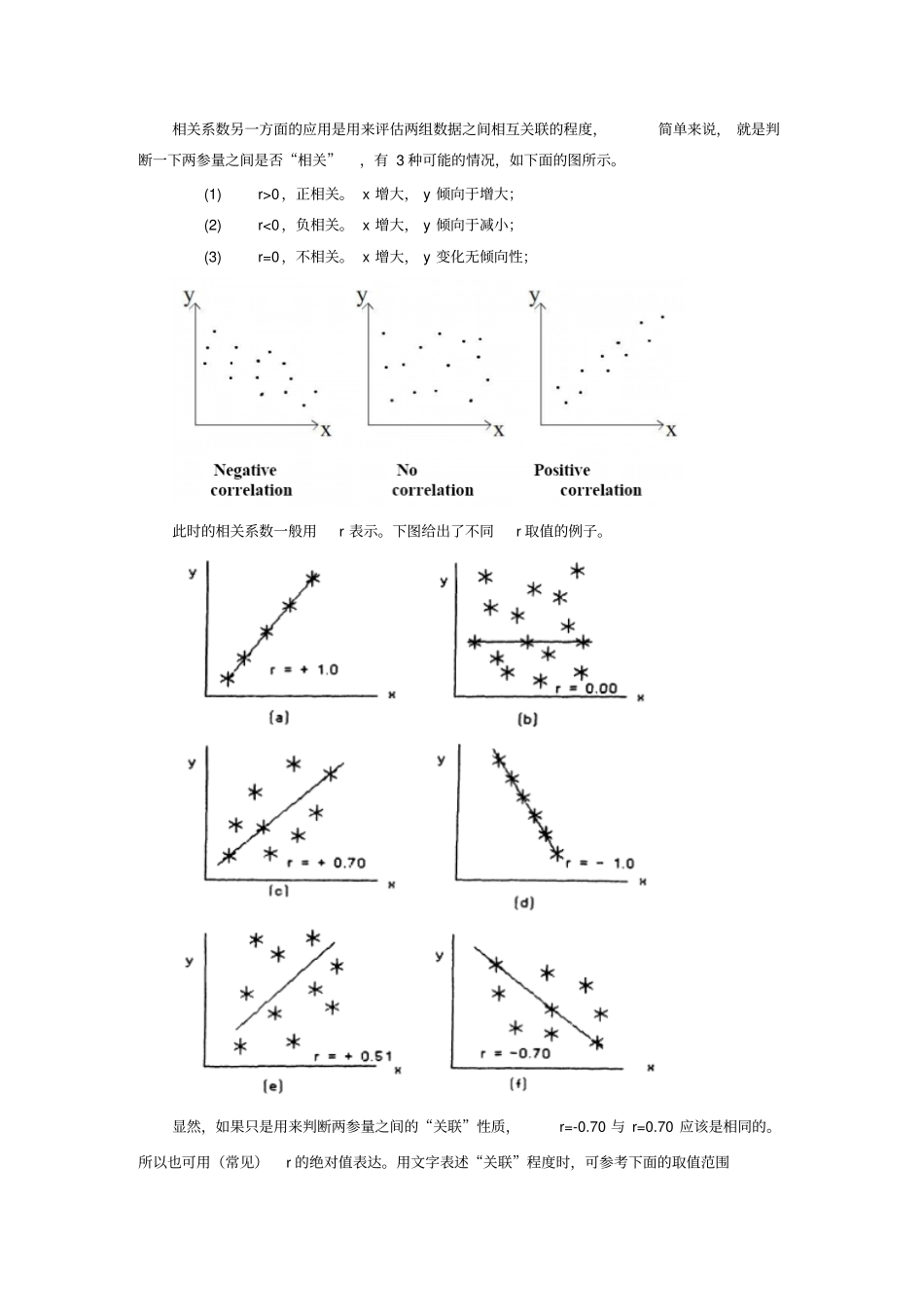
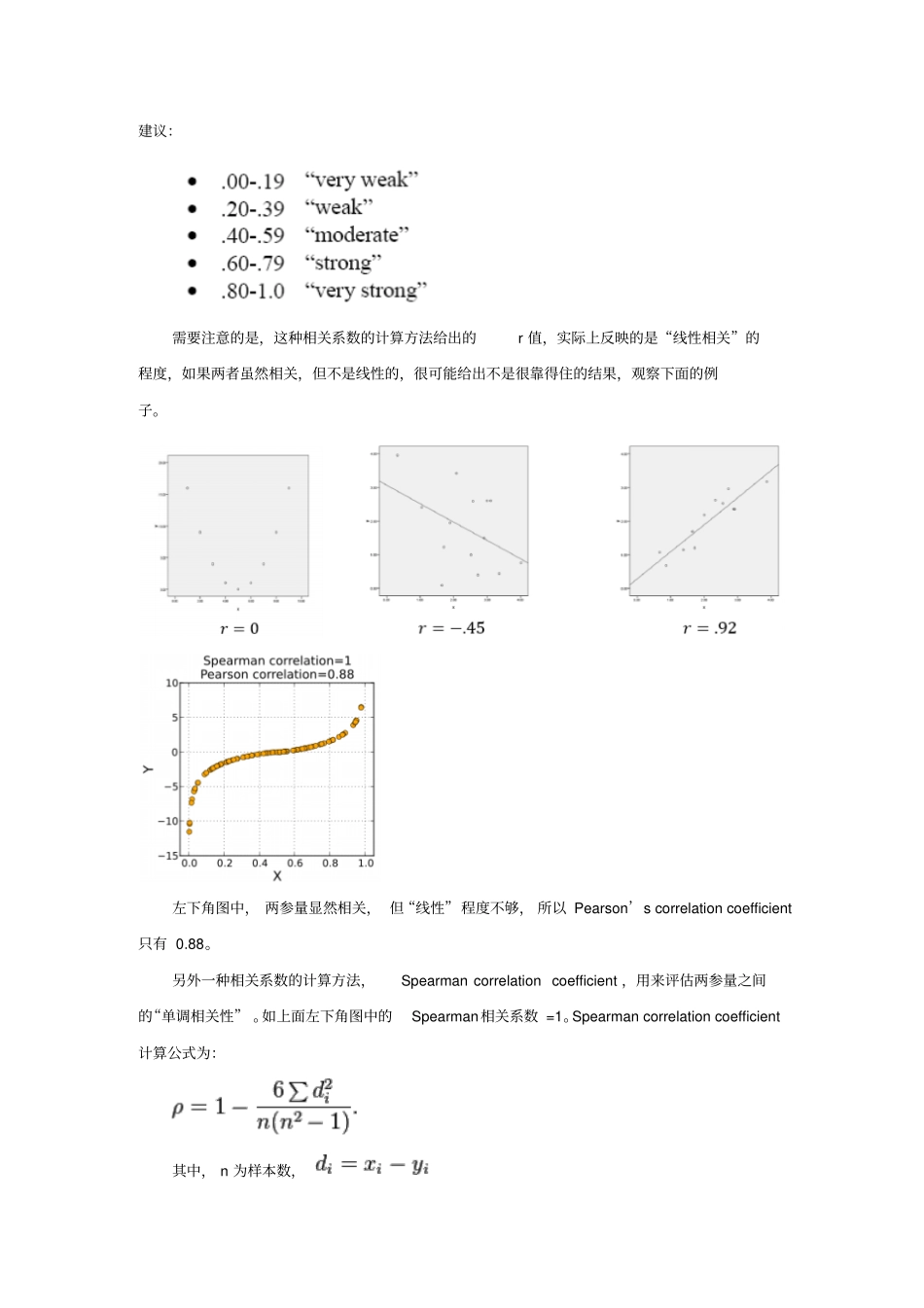
相关系数与 P 值的一些基本概念注:在期末论文写作过程中,关于相关系数与假设检验结果的表达方式,出现了一些概念问题。这篇文档的内容是对一些相关资料进行整理后的结果,供感兴趣的同学参考。如果需要更确切的定义,请进一步参阅统计分析类的教材。1.相关系数常用 Pearson’s correlation coefficient,计算公式与传统概念上的相同,即:常用符号 r 表示。 -1≤ r≤1 如果用于评估数据点与拟合曲线间的关联程度,则一般用相关系数的平方值表示,常用符号为2R,1R02典型示例如下图。2R相差不大,但显然数据规律完全不同。因此,一般需要结合拟合曲线图表给出2R ,才有参考价值。相关系数另一方面的应用是用来评估两组数据之间相互关联的程度,简单来说, 就是判断一下两参量之间是否“相关”,有 3 种可能的情况,如下面的图所示。(1)r>0,正相关。 x 增大, y 倾向于增大;(2)r<0,负相关。 x 增大, y 倾向于减小;(3)r=0,不相关。 x 增大, y 变化无倾向性;此时的相关系数一般用r 表示。下图给出了不同r 取值的例子。显然,如果只是用来判断两参量之间的“关联”性质,r=-0.70 与 r=0.70 应该是相同的。所以也可用(常见)r 的绝对值表达。用文字表述“关联”程度时,可参考下面的取值范围建议:需要注意的是,这种相关系数的计算方法给出的r 值,实际上反映的是“线性相关”的程度,如果两者虽然相关,但不是线性的,很可能给出不是很靠得住的结果,观察下面的例子。左下角图中, 两参量显然相关, 但“线性”程度不够, 所以 Pearson’s correlation coefficient只有 0.88。另外一种相关系数的计算方法,Spearman correlation coefficient ,用来评估两参量之间的“单调相关性” 。如上面左下角图中的Spearman相关系数 =1。Spearman correlation coefficient计算公式为:其中, n 为样本数,下面的图是一些例子:2. P 值( p-values)P 值是配对t检验(paired t-test)计算过程中得到的结果。用来评估前面所述相关程度计算结果的“显著程度” 。在常用统计软件SPSS 中, P 值( p-value,有时显示为Sig-value )的计算是建立在如下两个假设基础上的:无效假设( null hypothesis )0r:H 0,两参量间不存在“线性”关联。备择假设( alternative hypothesis )0r:H 1,两参量间存在“线性”关联。如果计算出的P 值很小, 比如为 0.001,则可说 “有非常显著的证据...