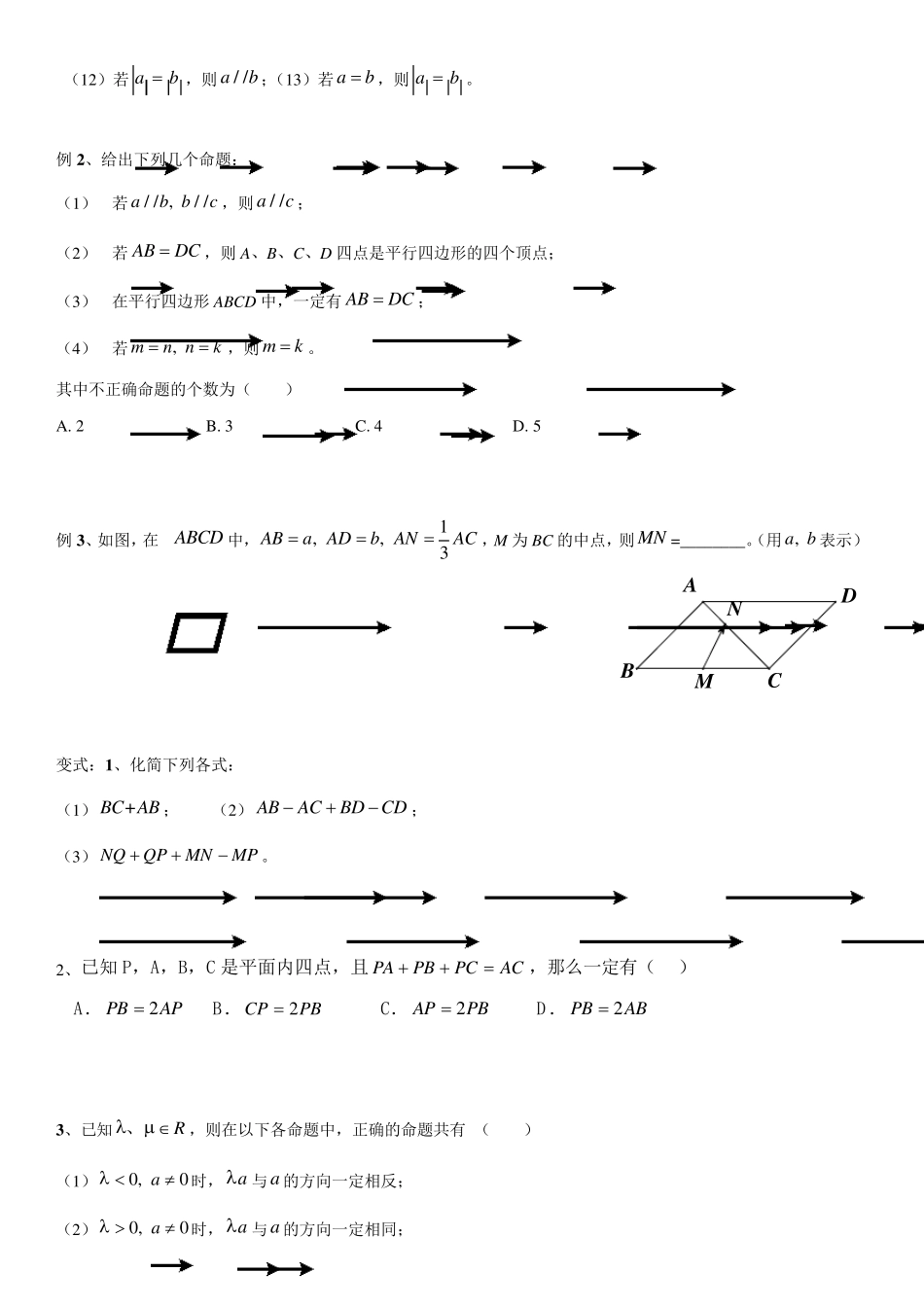
一、同步知识梳理 1 、向量:既有大小,又有方向的量.(注意零向量,单位向量) 数量:只有大小,没有方向的量. 有向线段的三要素:起点、方向、长度. 平行向量(共线向量):方向相同或相反的非零向量.零向量与任一向量平行. 相等向量:长度相等且方向相同的向量. 2 、向量加(减)法运算: ⑴三角形法则的特点:首尾相连. ⑵平行四边形法则的特点:共起点. ⑶三角形不等式:ababab. ⑷运算性质:①交换律:abba;②结合律:abcabc;③00aaa. 3 、向量数乘运算: ⑴实数 与向量a 的积是一个向量的运算叫做向量的数乘,记作 a. ①aa; ②当0 时,a的方向与a 的方向相同;当0 时,a的方向与a 的方向相反;当0 时,0a. ⑵运算律:① aa ;②aaa;③ abab. 二、同步例题分析 例 1 、判断下列命题的真假。 (1 )零向量是没有方向的;(2 )零向量与任一向量共线;(3 )零向量的方向是任意的;(4 )单位向量都是相等的向量;(5 )向量AB 与向量BA 的长度相等;(6 )不相等的向量一定不平行;(7 )若两个单位向量共线,则必相等;(8 )向量就是有向线段;(9 )非零向量a 的单位向量是 aa;(1 0 )若/ /ab ,则ab;(1 1 )若 ab,则ab;ba C abCC (12)若ab,则/ /ab;(13)若ab,则ab。 例2 、给出下列几个命题: (1) 若/ / , / /ab bc ,则/ /ac ; (2) 若ABDC,则A、B、C、D 四点是平行四边形的四个顶点; (3) 在平行四边形 ABCD 中,一定有 ABDC; (4) 若, mn nk,则mk。 其中不正确命题的个数为( ) A. 2 B. 3 C. 4 D. 5 例3 、如图,在ABCD 中,1, , 3ABaADb ANAC,M 为 BC 的中点,则MN =________。(用 , a b 表示) 变式:1 、化简下列各式: (1)+BC AB ; (2)ABACBDCD; (3)NQQPMNMP。 2、已知 P,A,B,C 是平面内四点,且ACPCPBPA,那么一定有( ) A.APPB2 B.PBCP2 C.PBAP2 D .ABPB2 3 、已知R 、,则在以下各命题中,正确的命题共有 ( ) (1)0, 0a 时,a与a 的方向一定相反; (2)0, 0a 时,a与a ...