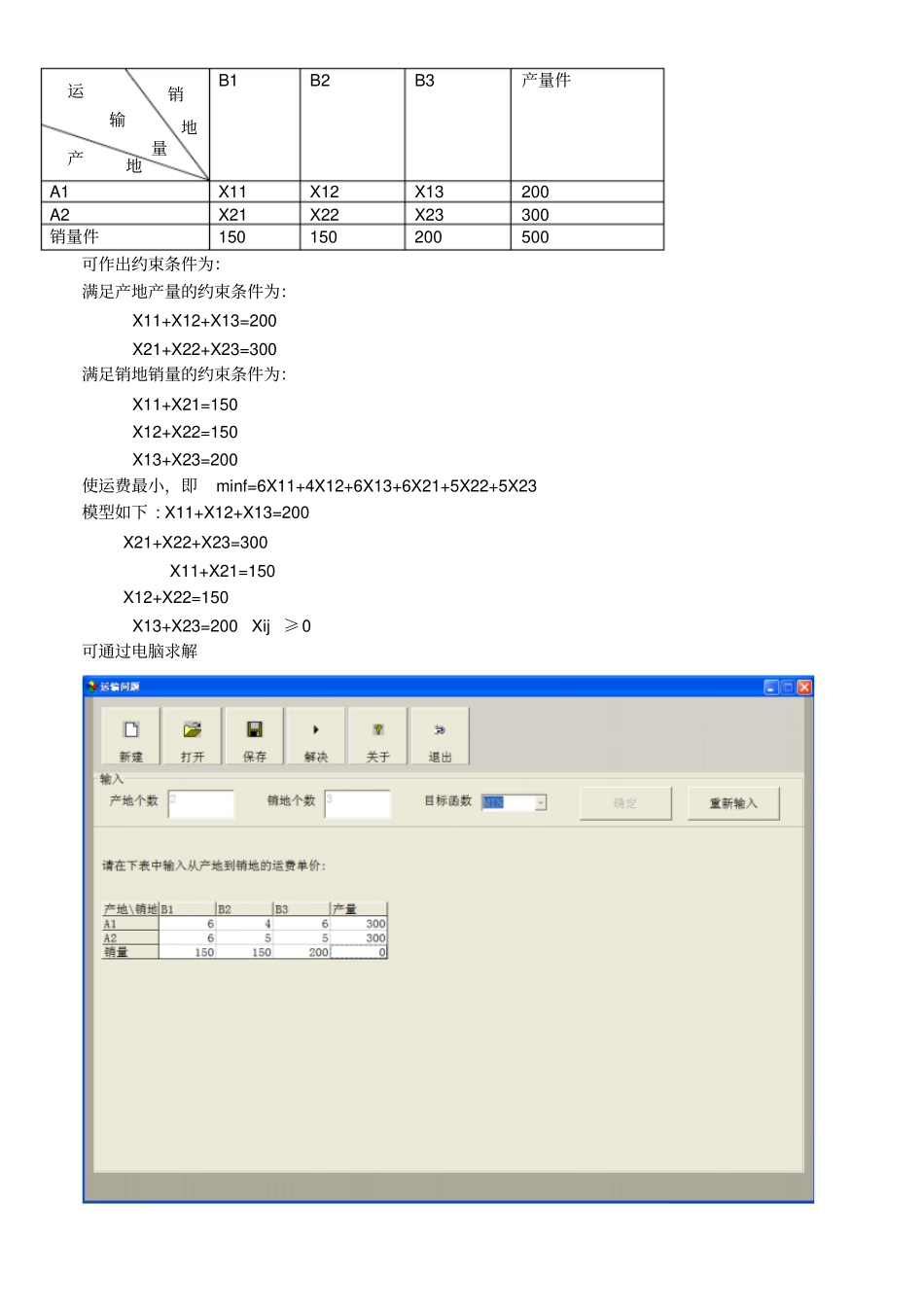
管理运筹学线性规划与运输问题线性规划某工厂在计划期内要安排Ⅰ、Ⅱ两种产品的生产,生产单位产品所需的设备台时及AB 两种原材料的消耗及资源的限制如下表:ⅠⅡ资源限制设备1 1 300 台时原料 A 2 1 400 ㎏原料 B 0 1 250 ㎏工厂每生产一单位产品Ⅰ可获利50 元,每生产一单位Ⅱ产品可获利100 元,为工厂应分别生产多少单位产品Ⅰ和产品Ⅱ才能使获利最多?解答:1、 建模:用变量X1 和 X2 来分别表示生产多少单位产品Ⅰ和产品Ⅱ,用X1 和 X2 的线性函数来表示工厂所要求的最大利润目标:MaxZ=50X1+100X2 其他约束条件为:X1+X2 ≤300 2X1+X2 ≤400 X2 ≤250 X1 ≥0;X2 ≥0 2、 求解计算:通过图解法,可以算得当X1=50,X2=250时, Z=27500 ,这说明该厂生产产品Ⅰ50 千克,产品Ⅱ 250 千克,既有最大利润,此时消耗设备台时300,原料A 350 千克,原料B 250 千克。3、 电脑求解:运输模型某公司从两个产地A1 、A2 将物品运往三个销地B1、B2、B3 ,各产地的产量、各销地的销量和各产地运往各销地的每件物品的运费如下表:B1 B2 B3 产量/件A1 6 4 6 200 A2 6 5 5 300 销量/件150 150 200 应如何调运,使得总运费最小?解答:1、 建模:通读题意可知,两个产地的总销量与三个销地的总销量相等,这是一个产销平衡的运输问题。设 Xij 表示从产地Ai 调运到 Bj 的运输量( i=1,2。j=1,2,3 )如 X12 表示由 A1 调运到 B2 的物品的数量,现将安排的运输量安排如下:销地运费单价产地B1 B2 B3 产量件A1 X11 X12 X13 200 A2 X21 X22 X23 300 销量件150 150 200 500 可作出约束条件为:满足产地产量的约束条件为: X11+X12+X13=200 X21+X22+X23=300 满足销地销量的约束条件为: X11+X21=150 X12+X22=150 X13+X23=200 使运费最小,即minf=6X11+4X12+6X13+6X21+5X22+5X23 模型如下 : X11+X12+X13=200 X21+X22+X23=300 X11+X21=150 X12+X22=150 X13+X23=200 Xij≥0 可通过电脑求解销地运输量产地管理运筹学图与网络问题——最短路问题图表示 V1 到 V6 的最短路(1)给起始点 V1 标以( 0,s),表示从 V1 到 V2 的距离为 0,V1 是起始点。(2)这时已标定点集合I={V1},未标定点的集合J={V2,V 3,V 4,V 5,V 6},弧集合{(Vi,Vj)|Vi∈I,Vj∈J}={(V1,V 2),(V 1,V3),(V 1,V4)...