纠错编码习题解答重点讲义资料

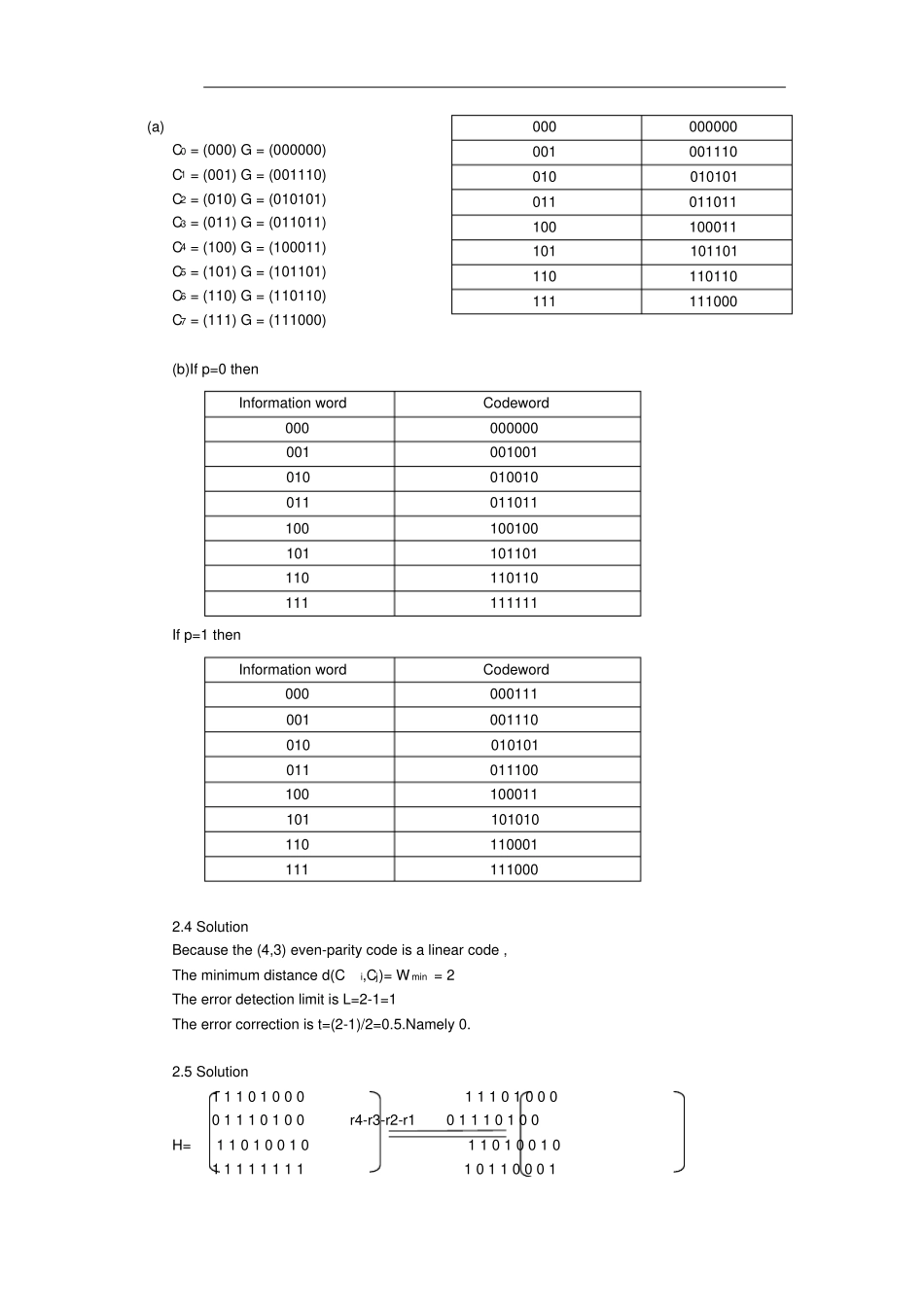
纠错编码习题解答第一章1.1 Solution: p=0.05 (1)The correct decoding Pc is Pc= P0 =C40p0 (1-p)4=0.8145 (2)The decoding error Pe is P e = P 2+P4 = C42p2(1-p)2 + C44p4(1-p) 0 = 0.0135 (3)The decoding failure Pf is Pf= C41p(1-p) 3 + C43p3(1-p) = 0.1720 1.2 Solution: Because the success rate does not fall below 99%,then the decoding failure Pf<1% .And p<<1, Pf = P1 = n*0.001*0.999n-1 < 0.01 So n<=10 .then the maximum blocklength n such that the success rate does not fall below 99% is 10. 1.3 Solution: p=0.01 Pf = P2 = C42p2(1-p)2 = C42 * 0.01 2 * 0.992 = 0.000588 So the decoding failure rate is 0.000588. 1.4 Solution: (a)Error: There is one error (b)Correct (c)Failure (d)Error: There is two error1.5 Solution: S1 = v1+v 2+v 3+v4+v 6+v 8+v 9+v12S2 = v2+v 3+v 4+v5+v 7+v 9+v 10+v13S3 = v3+v 4+v 5+v6+v 8+v 10+v 11+v 14S4 = v1+v 2+v 3+v5+v 7+v 8+v 11+v15Error pattern e Error Syndrome s (e1 ,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11 ,e12,e13,e14 ,e15) (s1,s2,s3,s4) 0000 0000 0000 000 0000 0000 0000 0000 001 0001 0000 0000 0000 010 0010 0000 0000 0000 100 0100 0000 0000 0001 000 1000 0000 0000 0010 000 0011 0000 0000 0100 000 0110 0000 0000 1000 000 1100 0000 0001 0000 000 1011 0000 0010 0000 000 0101 0000 0100 0000 000 1010 0000 1000 0000 000 0111 0001 0000 0000 000 1110 0010 0000 0000 000 1111 0100 0000 0000 000 1101 1000 0000 0000 000 1001 1.6 Solution (1)s=(0000) ~e = 0000 0000 0000 000 ~c= ~e+v 1 = (000000000000000)+(100010011001001)= (100010011001001) (2)s=(1011) ~e = 0000 0001 0000 000 ~c= ~e+v 2 = (000000010000000)+(001001110100110)= (001001100100110) 1.7 Solution (1) v=(1011 110) s=(110) ~e = (001 0000) ~c=(1001 110) (2) v=(1100 110) s=(100) ~e = (0000 100) ~c=(1100 010) (3) v=(0001 011)...