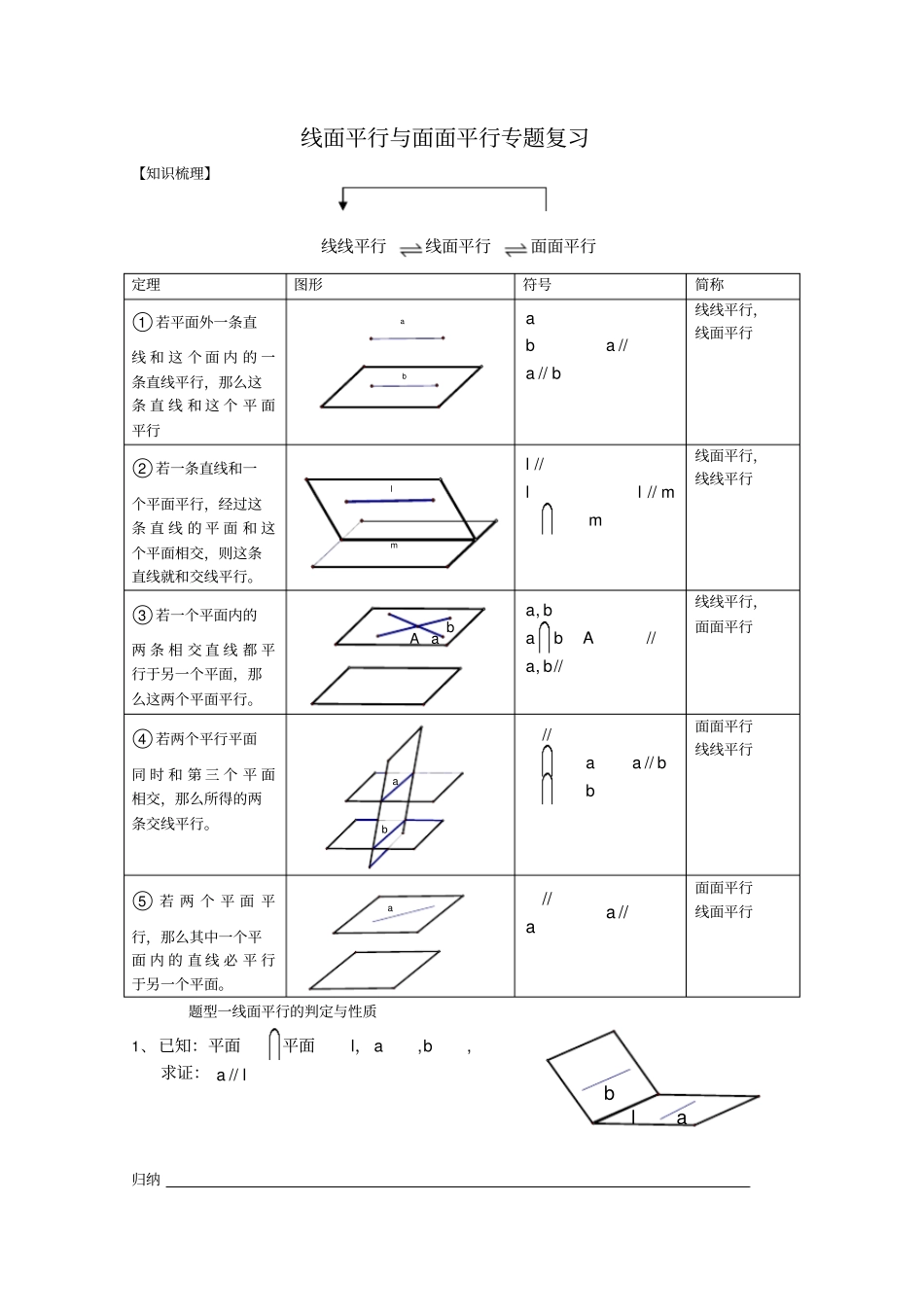
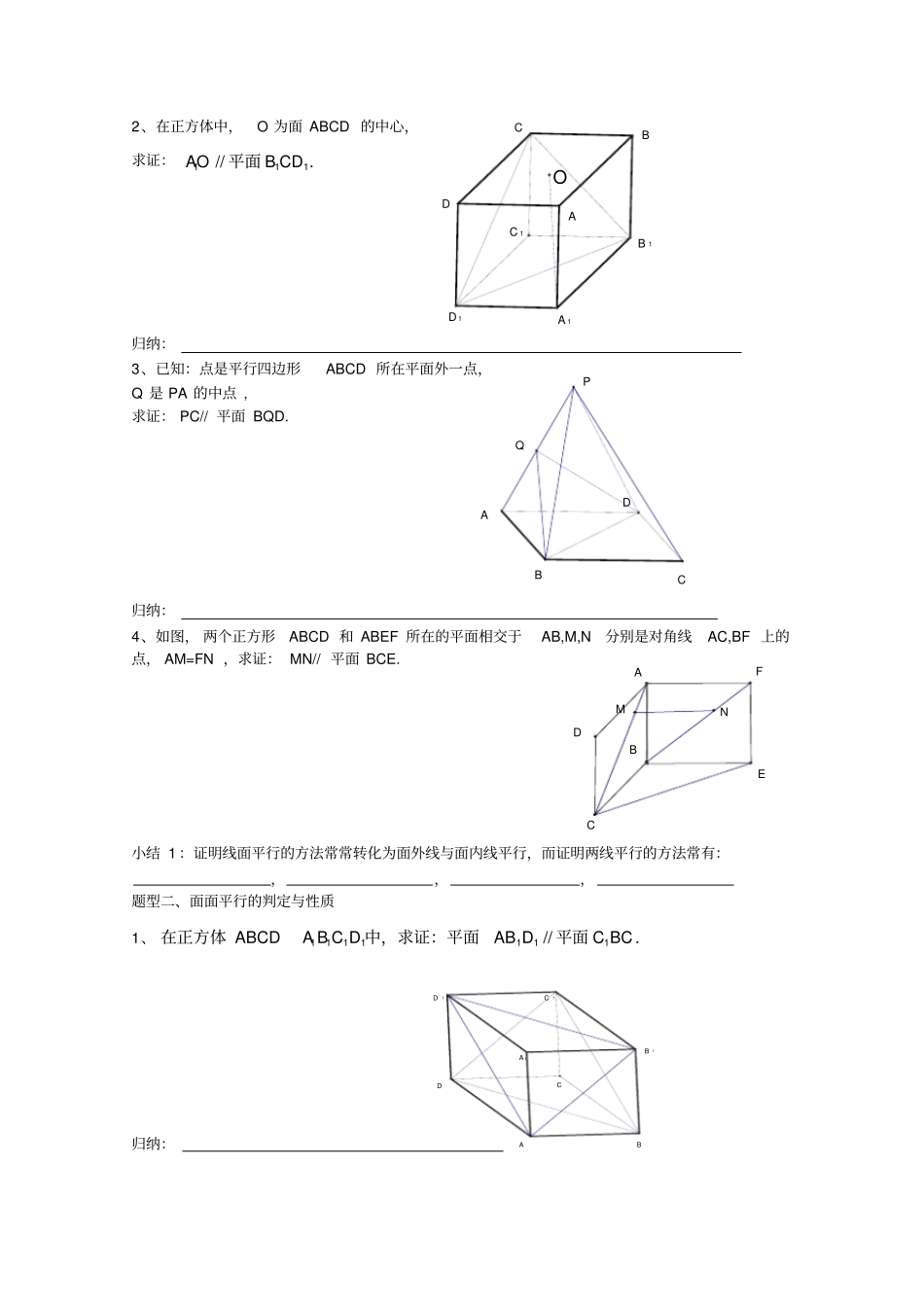
mlbabaA aba线面平行与面面平行专题复习【知识梳理】线线平行线面平行面面平行题型一线面平行的判定与性质1、,,//labal已知:平面平面,求证:归纳定理图形符号简称○1 若平面外一条直线 和 这 个 面 内 的 一条直线平行,那么这条 直 线 和 这 个 平 面平行////abaab线线平行,线面平行○2 若一条直线和一个平面平行,经过这条 直 线 的 平 面 和 这个平面相交,则这条直线就和交线平行。////lllmm线面平行,线线平行○3 若一个平面内的两 条 相 交 直 线 都 平行于另一个平面,那么这两个平面平行。,//,//a babAa b线线平行,面面平行○4 若两个平行平面同 时 和 第 三 个 平 面相交,那么所得的两条交线平行。////aabb面面平行线线平行○5若 两 个 平 面 平行,那么其中一个平面 内 的 直 线 必 平 行于另一个平面。////aa面面平行线面平行lbaDCBAD 1C 1B 1A 1OQDCBAPBNMDAFECC1B1A 1D1DCBA2、在正方体中,O 为面 ABCD 的中心,求证:111//.AOB CD平面归纳:3、已知:点是平行四边形ABCD 所在平面外一点,Q 是 PA 的中点 , 求证: PC// 平面 BQD. 归纳:4、如图, 两个正方形ABCD 和 ABEF 所在的平面相交于AB,M,N分别是对角线AC,BF 上的点, AM=FN ,求证: MN// 平面 BCE. 小结 1 :证明线面平行的方法常常转化为面外线与面内线平行,而证明两线平行的方法常有:,,,题型二、面面平行的判定与性质1、1111111//.ABCDA B C DAB DC BC在正方体中,求证:平面平面归纳:DA1C1CB1B11111111111,,:(1)//;(2)//.ABCA B CDACBCAB DDACB DABC D2、如图 已知正三棱柱中,点为的中点 求证平面为的中点,求证:平面平面归纳:3//,,,,,,////AB CDACBDE FABCDEF、已知平面平面 ,是异面直线,分别为,的中点,求证:归纳:练习:1.如图,ED,分别是正三棱柱111ABCA B C 的棱1AA 、11B C 的中点,求证:1//A E平面1BDC ;2.在直三棱柱111CBAABC中,E 、 F 分别为11A C 、11B C 的中点 , D 为棱1CC 上任一点 . 求证:直线 EF ∥平面 ABD ;3、如图, 在正方体1111ABCDA B C D 中, E ,F 分别是棱 BC ,11C D 的中点, 求证: EF //平面11BB D D .C 1 A B C D E F A 1 B 1 第 2 题FEDBCA1A1B1D1CFEABCD4. 如图, 在四棱锥 PABCD 中, ABCD 是平行四边形, M , N 分别是 AB ...