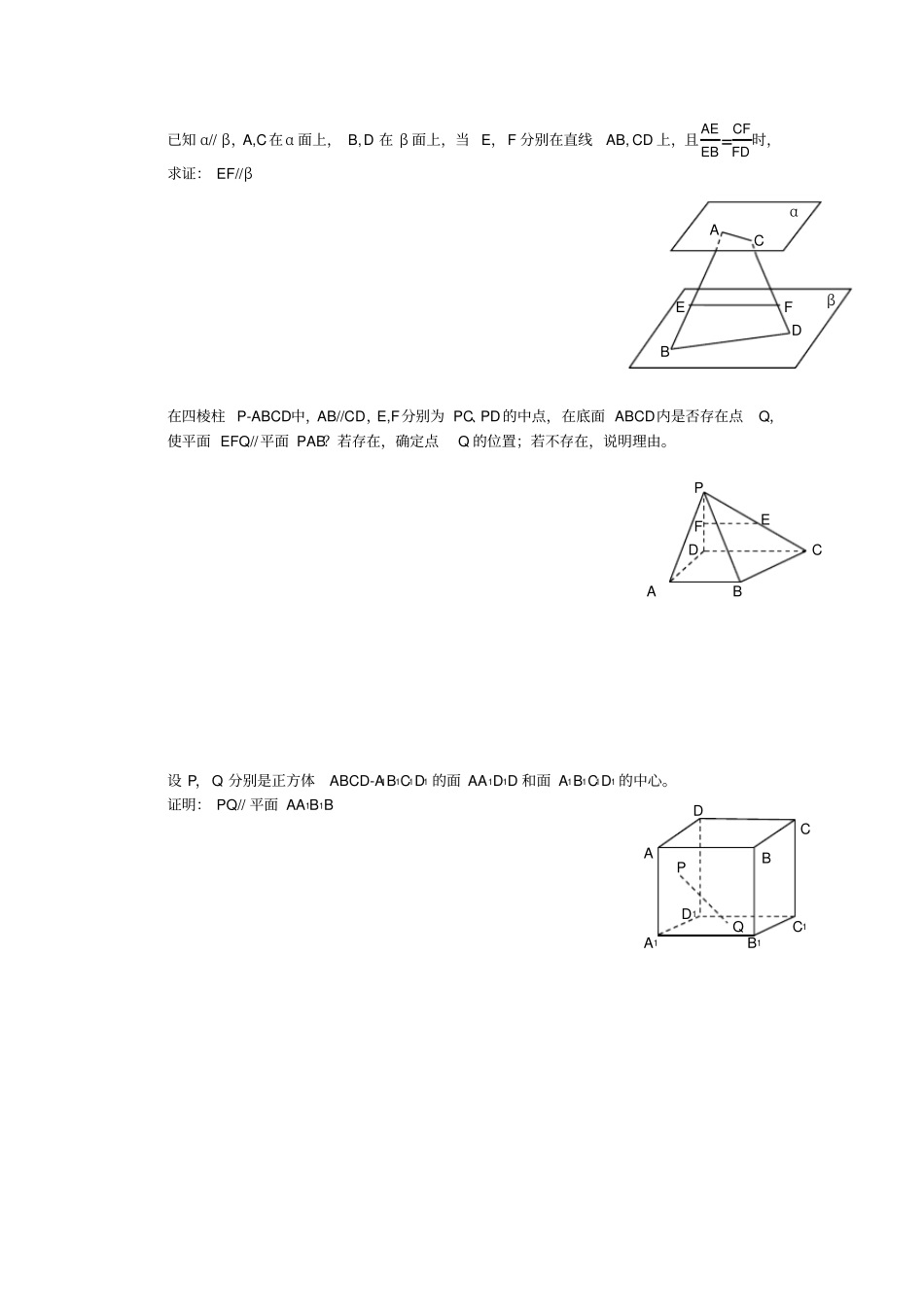
线、面平行习题集如图所示的几何体中,ABC 是任意三角形,AE//CD,且AE=AB=2a,CD=a,F 为 BE的中点。求证: DF//平面 ABC 如图,已知P 是平行四边形ABCD所在平面外一点,M、 N 分别是 AB、PC的中点。(1)求证: MN// 平面 PAD;(2)若 MN=BC=4, PA = 4√3,求异面直线PA与 MN 所成的角的大小。(09 年山东文) 如图, 在直四棱柱ABCD-A1B1C1D1 中,底面 ABCD为等腰梯形, AB//CD,AB=4,BC=CD=2,AA1=2,E,E1 分别是棱 AD,AA1 的中点。 设 F 是棱 AB 的中点。证明:直线 EE1// 平面 FCC1A B C D E F A B D C P N M C E D F A A1E1B B1C1D1已知 α// β,A,C在α 面上, B,D 在 β 面上,当 E,F 分别在直线AB, CD 上,且AEEB=CFFD时,求证: EF//β在四棱柱 P-ABCD中,AB//CD,E,F分别为 PC、PD的中点,在底面 ABCD内是否存在点Q,使平面 EFQ//平面 PAB?若存在,确定点Q 的位置;若不存在,说明理由。设 P,Q 分别是正方体ABCD-A1B1C1D1 的面 AA1D1D 和面 A1B1C1D1 的中心。证明: PQ// 平面 AA1B1B A αβC B D F E D F A B C E P B C A1B1C1D1A Q P D