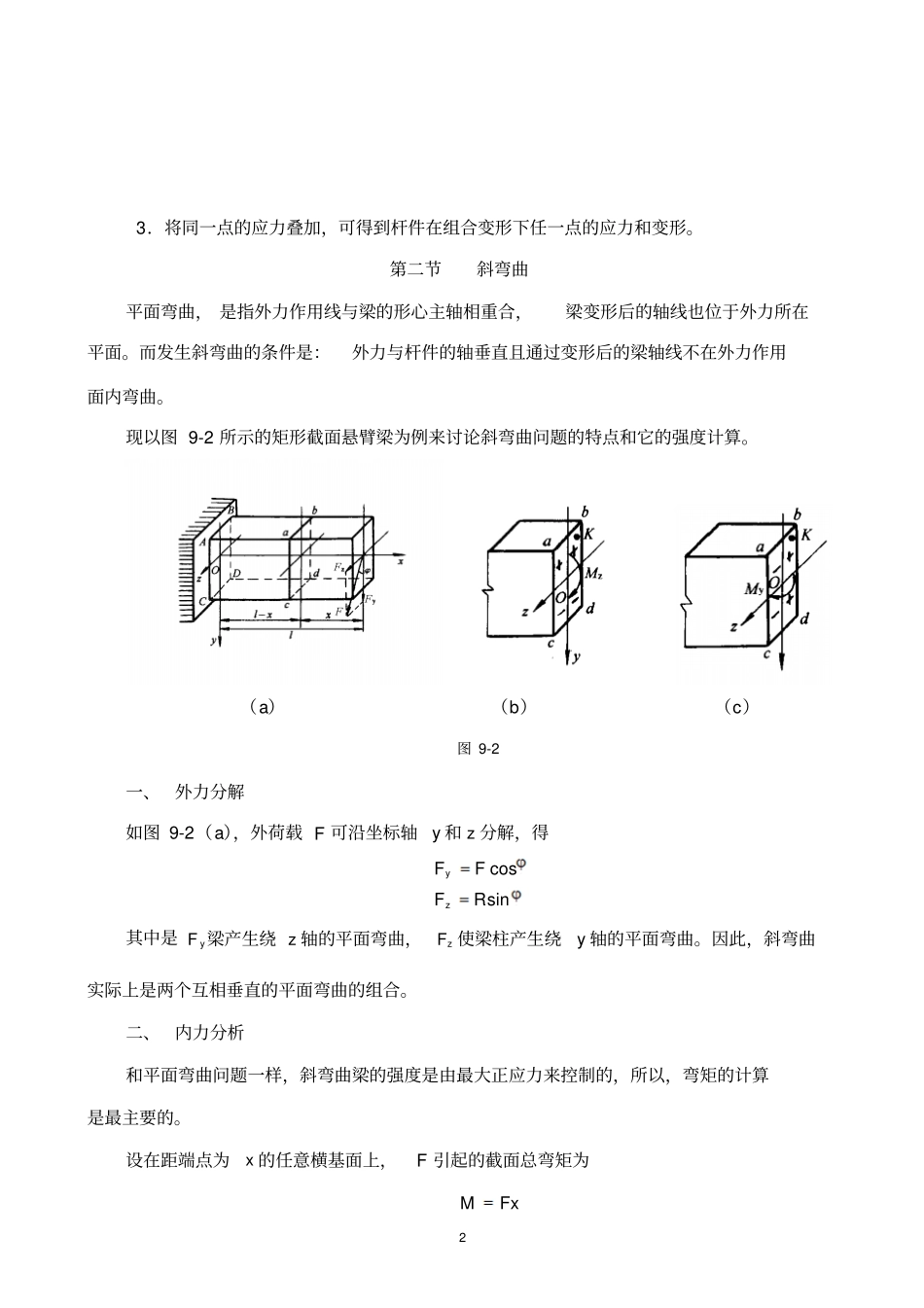
1 第 9 章 组合变形的强度计算学习目标:1.了解组合变形的概念,以及构件受力和变形特点。2.理解截面核心的概念及简单图形截面核心的位置。3.掌握斜弯曲、偏心拉压时构件的应力计算及强度条件。第一节组合变形的概念一、组合变形的概念在现实生活中有些杆件的受力情况较为复杂,所引起的变形不止是单一的基本变形,而是几种基本变形同时产生。如图9-1(a)所示的挡土墙结构,除了本身引起的压缩变形外,还有土压力引起的弯曲变形。图9-1(b)所示的单层厂房牛腿柱,所受的吊车轮压荷载和柱的轴线不重合,因而柱为偏心受压,同时产生压缩和弯曲两种基本变形。由两种或两种以上的基本变形组合而成的变形,称为组合变形。图 9-1 解决组合变形的强度问题可用叠加法,其分析步骤为:1.将杆件的组合变形分解为基本变形;2.计算杆件在每一种基本变形情况下所产生的应力和变形;( a)2 3.将同一点的应力叠加,可得到杆件在组合变形下任一点的应力和变形。第二节斜弯曲平面弯曲, 是指外力作用线与梁的形心主轴相重合,梁变形后的轴线也位于外力所在平面。而发生斜弯曲的条件是:外力与杆件的轴垂直且通过变形后的梁轴线不在外力作用面内弯曲。现以图 9-2 所示的矩形截面悬臂梁为例来讨论斜弯曲问题的特点和它的强度计算。(a)(b)(c)图 9-2 一、外力分解如图 9-2(a),外荷载 F 可沿坐标轴y 和 z 分解,得sincosRFFFzy其中是yF 梁产生绕 z 轴的平面弯曲,zF 使梁柱产生绕y 轴的平面弯曲。因此,斜弯曲实际上是两个互相垂直的平面弯曲的组合。二、内力分析和平面弯曲问题一样,斜弯曲梁的强度是由最大正应力来控制的,所以,弯矩的计算是最主要的。设在距端点为x 的任意横基面上,F 引起的截面总弯矩为FxM3 两个分力yF 和zF 引起的弯矩值为coscosMxFxFMyZsinsinMxFxFMzy三、应力计算在该横截面上任意点K 处(相应坐标zy、 ) ,由yM和ZM引起的正应力为IzyM ZMz.yyMyIzMy.由叠加原理,任意点K 的正应力为yyZZMyMzKIzMIyM..(9-1)代入总弯矩,可得)sincos(ZIyIMyZK(9-2)式中的yI 和zI 为横截面形心主轴z 和 y 的惯线矩;y 和 z 为 K 点坐标;具体计算中,zy、、M均以绝对值代入,而K 的正负号,可通过K 点所在位置直观判断。如图9-2(c)所示。四、强度条件1.中性轴位置因中性轴上各点正应力均为零,则由式(9-2) 可得0sincosyZIyI当0y 1时,0z 1,说明中性轴是通过截面形心的直线。因此有4 ...