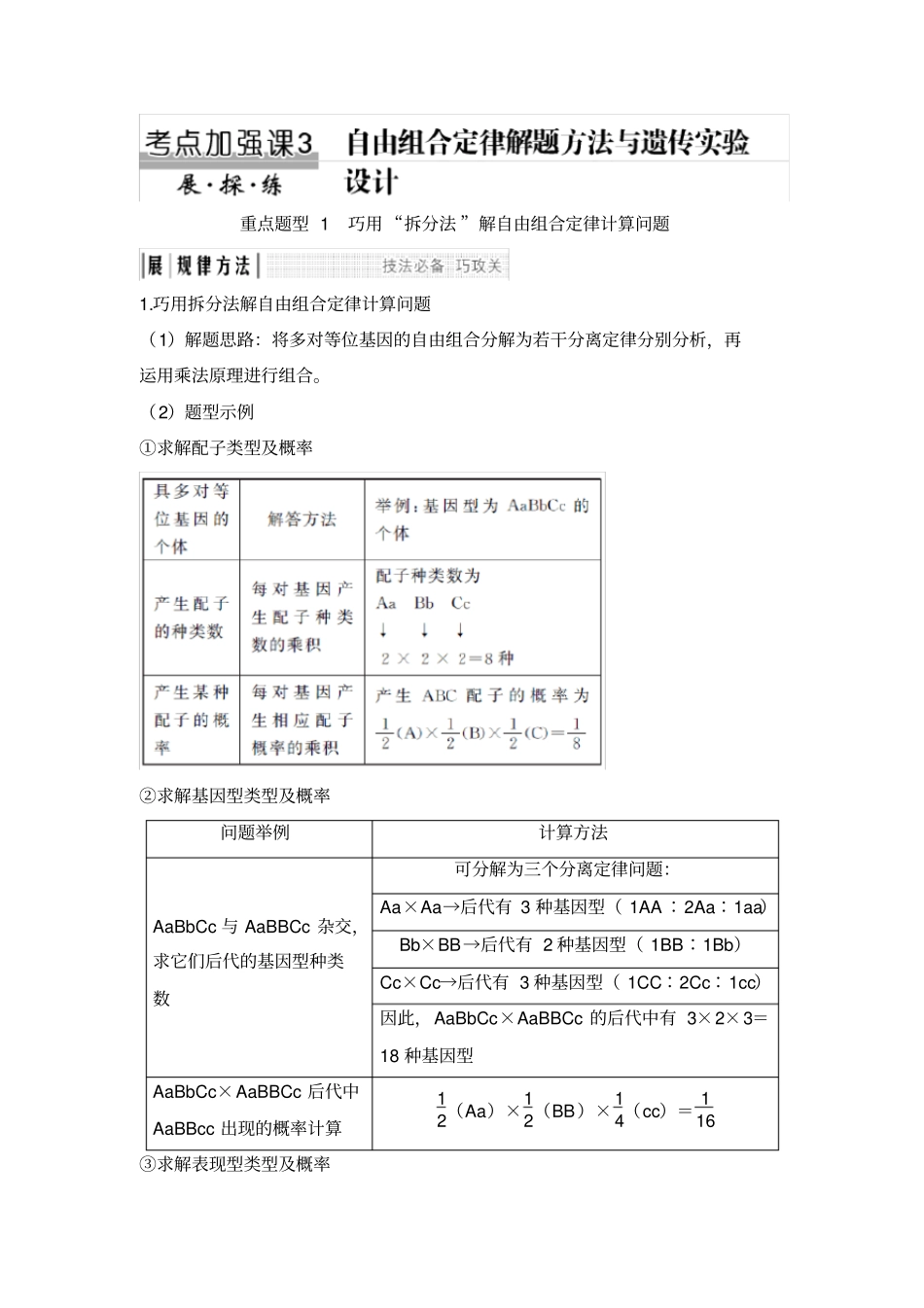
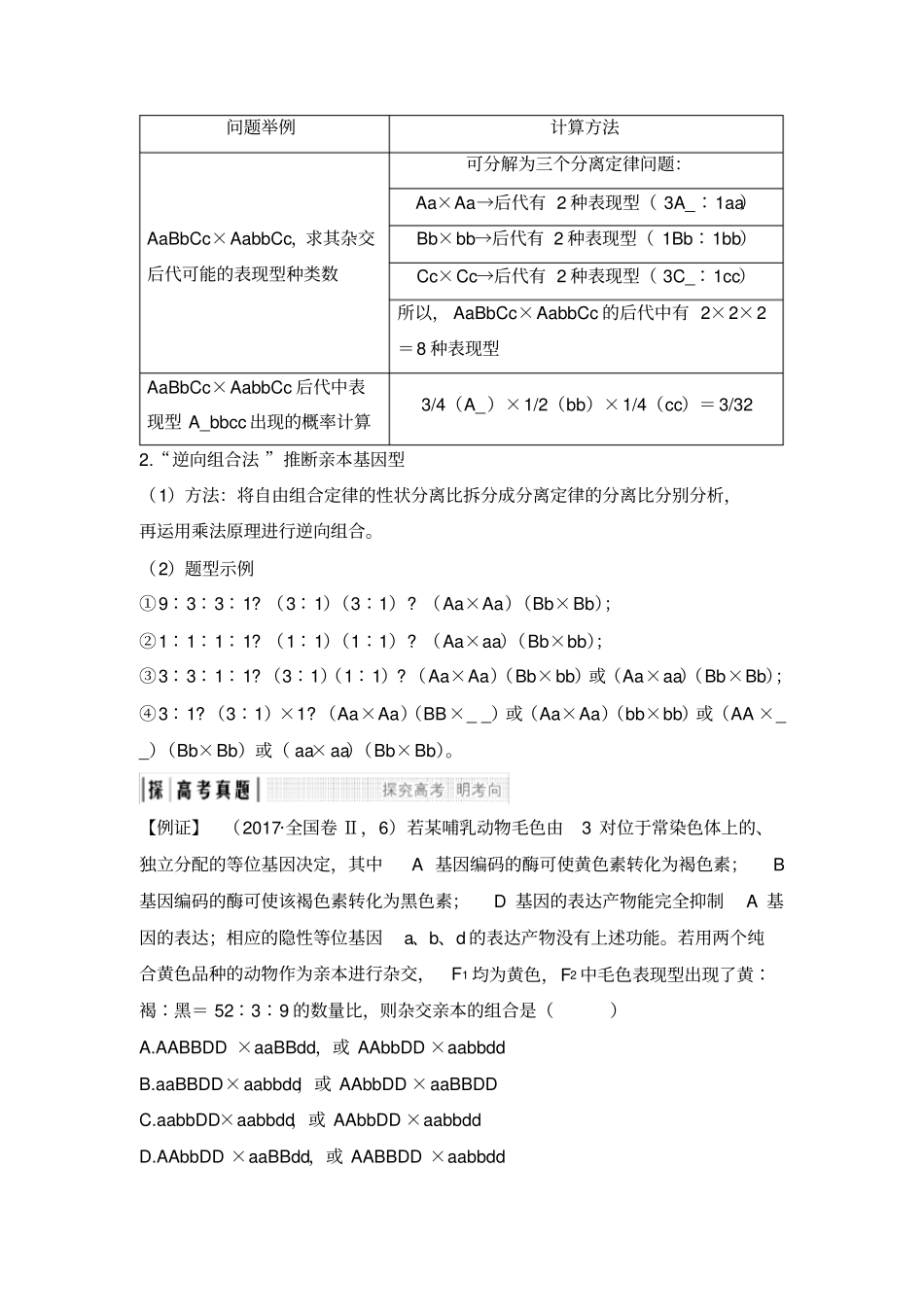
重点题型 1巧用 “拆分法 ”解自由组合定律计算问题1.巧用拆分法解自由组合定律计算问题(1)解题思路:将多对等位基因的自由组合分解为若干分离定律分别分析,再运用乘法原理进行组合。(2)题型示例①求解配子类型及概率②求解基因型类型及概率问题举例计算方法AaBbCc 与 AaBBCc 杂交,求它们后代的基因型种类数可分解为三个分离定律问题:Aa×Aa→后代有 3 种基因型( 1AA ∶2Aa∶1aa)Bb×BB→后代有 2 种基因型( 1BB∶1Bb)Cc×Cc→后代有 3 种基因型( 1CC∶2Cc∶1cc)因此,AaBbCc×AaBBCc 的后代中有 3×2×3=18 种基因型AaBbCc×AaBBCc 后代中AaBBcc 出现的概率计算12(Aa)×12(BB)× 14(cc)= 116③求解表现型类型及概率问题举例计算方法AaBbCc×AabbCc,求其杂交后代可能的表现型种类数可分解为三个分离定律问题:Aa×Aa→后代有 2 种表现型( 3A_∶1aa)Bb×bb→后代有 2 种表现型( 1Bb∶1bb)Cc×Cc→后代有 2 种表现型( 3C_∶1cc)所以, AaBbCc×AabbCc 的后代中有 2×2×2=8 种表现型AaBbCc×AabbCc 后代中表现型 A_bbcc 出现的概率计算3/4(A_)×1/2(bb)×1/4(cc)= 3/32 2.“逆向组合法 ”推断亲本基因型(1)方法:将自由组合定律的性状分离比拆分成分离定律的分离比分别分析,再运用乘法原理进行逆向组合。(2)题型示例①9∶3∶3∶1? (3∶1)(3∶1)? (Aa×Aa)(Bb×Bb);②1∶1∶1∶1? (1∶1)(1∶1)? (Aa×aa)(Bb×bb);③3∶3∶1∶1? (3∶1)(1∶1)? (Aa×Aa)(Bb×bb)或(Aa×aa)(Bb×Bb);④3∶1? (3∶1)×1? (Aa×Aa)(BB×_ _)或(Aa×Aa)(bb×bb)或(AA ×_ _)(Bb×Bb)或( aa× aa)(Bb×Bb)。【例证】(2017·全国卷 Ⅱ,6)若某哺乳动物毛色由3 对位于常染色体上的、独立分配的等位基因决定,其中A 基因编码的酶可使黄色素转化为褐色素;B基因编码的酶可使该褐色素转化为黑色素;D 基因的表达产物能完全抑制A 基因的表达;相应的隐性等位基因a、b、d 的表达产物没有上述功能。若用两个纯合黄色品种的动物作为亲本进行杂交,F1 均为黄色,F2 中毛色表现型出现了黄∶褐∶黑= 52∶3∶9 的数量比,则杂交亲本的组合是()A.AABBDD ×aaBBdd,或 AAbbDD ×aabbdd B.aaBBDD×aabbdd,或 AAbbDD ×aaBBDD C.aabbDD×aabbdd,或 AAbbDD ×aabbdd D.AAbbDD ×aaBBdd,或 AABBDD ×aabbd...