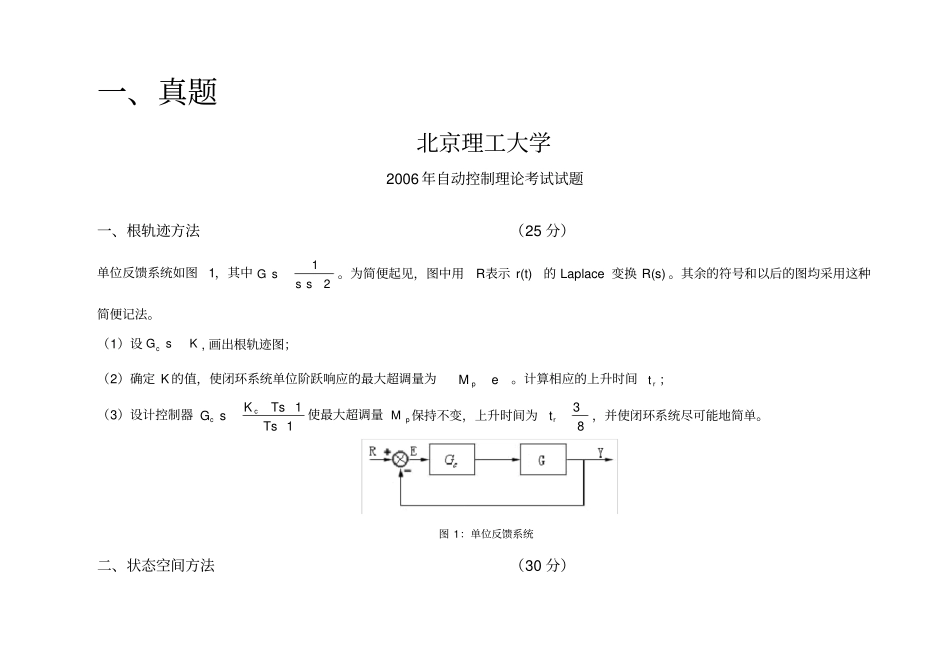
北京理工 大学自动化 学院自动化 专业—— 2019 年真题及解析科目一:代码 810 科目名称自动控制理论一、真题北京理工大学2006 年自动控制理论考试试题一、根轨迹方法(25 分)单位反馈系统如图1,其中21sssG。为简便起见,图中用R表示 r(t)的 Laplace 变换 R(s) 。其余的符号和以后的图均采用这种简便记法。(1)设KsGc, 画出根轨迹图;(2)确定 K 的值,使闭环系统单位阶跃响应的最大超调量为eM p。计算相应的上升时间rt ;(3)设计控制器11TsTsKsGcc使最大超调量pM保持不变,上升时间为83rt,并使闭环系统尽可能地简单。图 1:单位反馈系统二、状态空间方法(30 分)考虑系统DuCxyBuAxx。(1)先设210100100aaaA(ⅰ)证明:若2122101223,其中ssasasassf,则可通过状态空间中的线性变换Txx?,将状态空间表达式( 1)变为DuxCyuBxAx??????。(2)其中221001000?JAT 可取为222221112101T(ⅱ)设110001000A求AtJtee 和。(ⅲ) A同(ⅱ),100,011CBT判断系统的可控性和可观测性。若系统不可控或不可观测,确定不可控或不可观测的模态;(ⅳ) A,B,C 同(ⅲ), D=0,txxT ,1110是状态方程在初态0x下的解,证明0,30ttuetxxtT,并解释这个结果。(ⅴ)又设1100001000000001A B,C,D待定。若要通过状态反馈tKxtu配置系统的极点,至少需要几个独立的控制变量(即B 至少要有几个线性无关的列向量)?请说明理由。若要通过状态反馈tKxtu使闭环系统渐近稳定,至少需要几个独立的控制变量?请说明理由。三、频率响应分析(25 分)考虑图 2 所示的控制系统,其中sGsGsGc21,和均为最小相位系统,其渐近对数幅频特性曲线如图3,H(s)=1。图 2:由三个最小相位环节构成的反馈控制系统图 3:渐近对数幅频特性曲线(1)确定开环传递函数sHsGsGsGsGc210并画出其渐近对数幅频和相频特性曲线 (要求按图 3 中的尺寸自制两张对数坐标纸) ;(2)画出 Nyquist 曲线jG0;(3)由 Nyquist 曲线确定使闭环系统稳定的K 值,并用根轨迹方法验证;(4)求 K=1和 K=2时的稳态误差和加速度误差。四、非线性控制系统(25 分)系统的方框图如图4 所示,其中111132321KMM,,,所有的非线性特性均关于原点中心对称,21sssG。画出负倒特性曲线和线性部分sG的 Nyquist 图,以此分析系统是否存在自激振荡及其稳定性;如果存在自激振荡, 请计算输出ty的振幅和频率。图中死区、饱和特性和继电特性等非线性环节的描述函数分别...