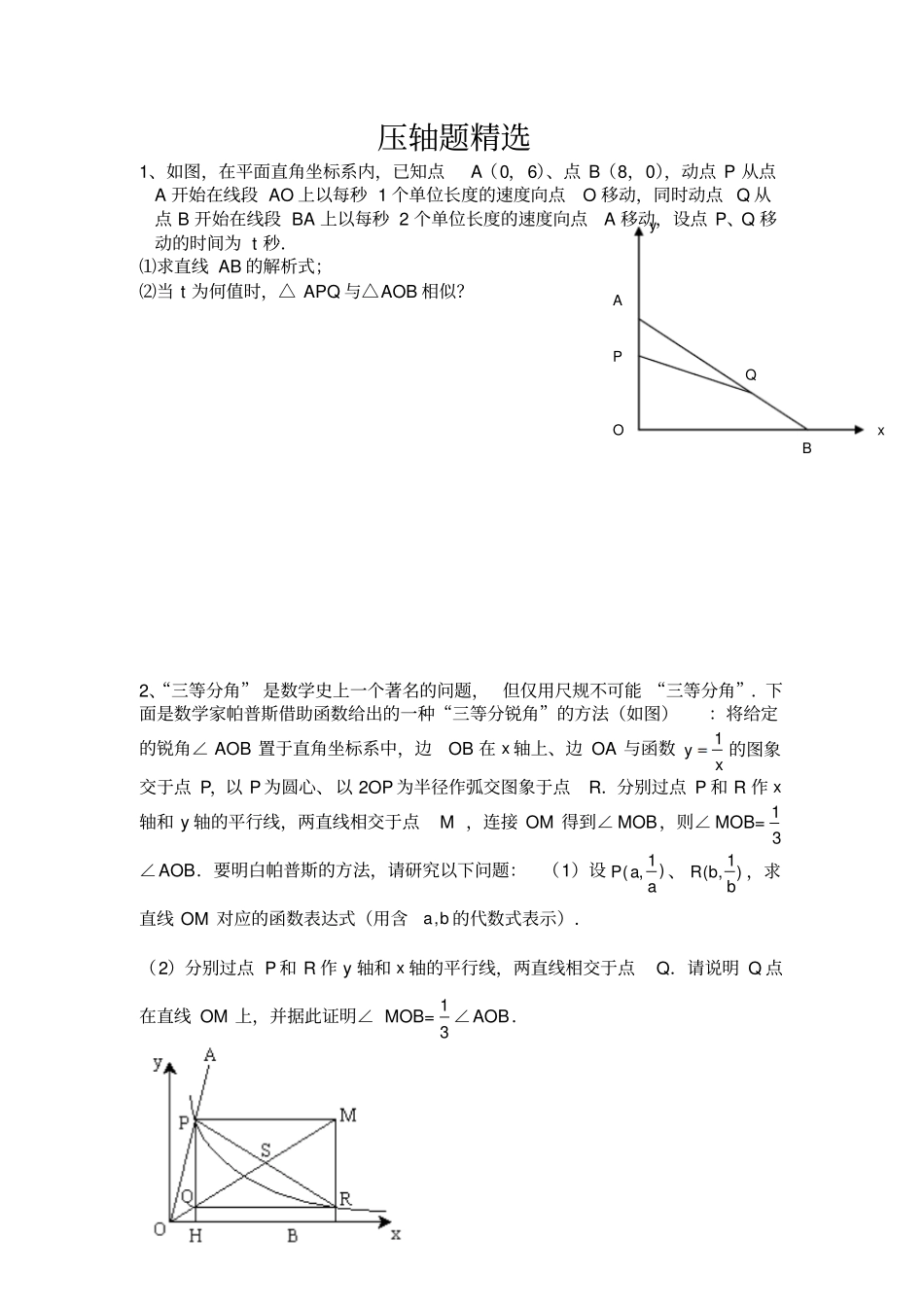
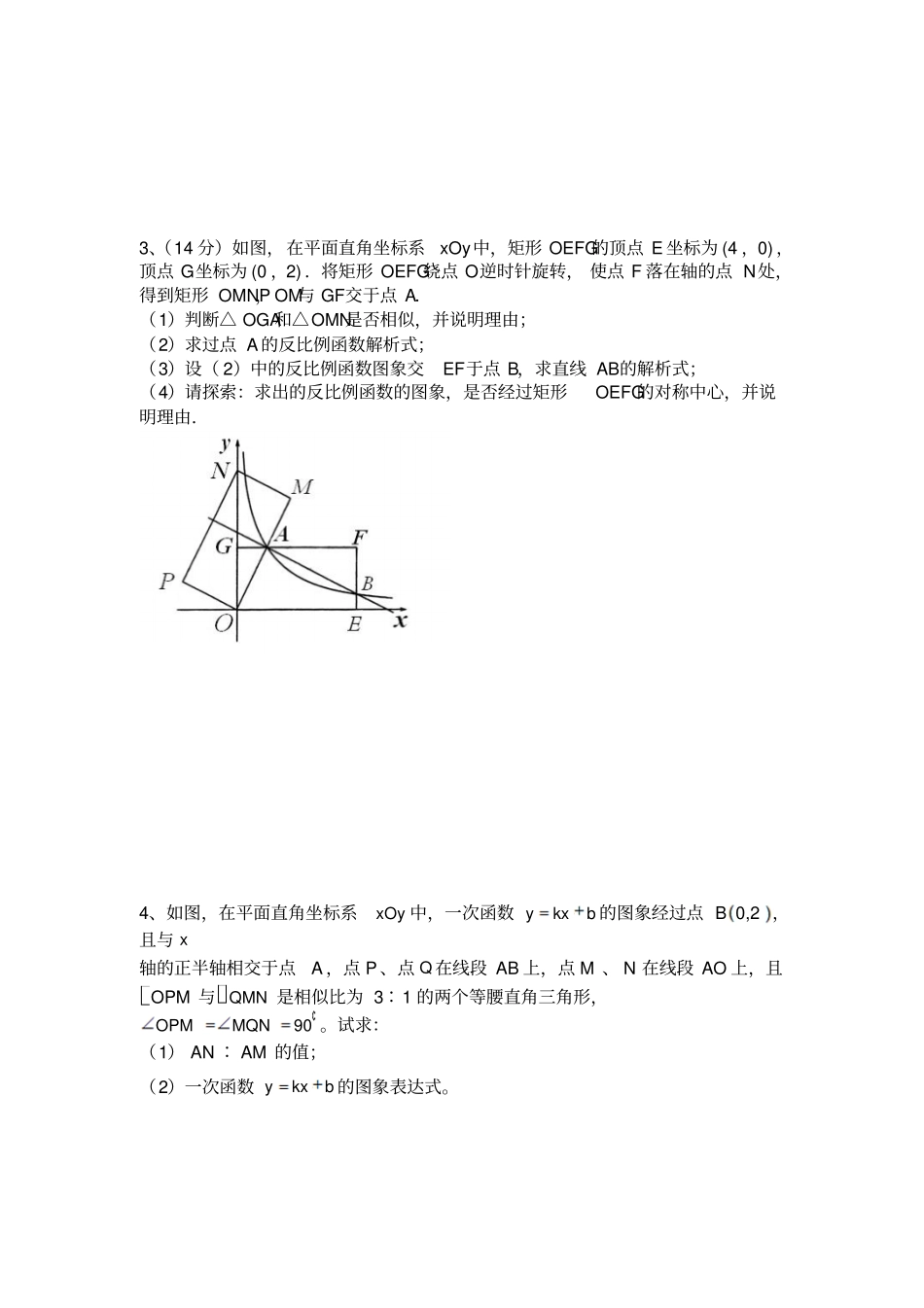
压轴题精选1、如图，在平面直角坐标系内，已知点A（0，6）、点 B（8，0），动点 P 从点A 开始在线段 AO 上以每秒 1 个单位长度的速度向点O 移动，同时动点 Q 从点 B 开始在线段 BA 上以每秒 2 个单位长度的速度向点A 移动，设点 P、Q 移动的时间为 t 秒．⑴求直线 AB 的解析式；⑵当 t 为何值时，△ APQ 与△AOB 相似
2、“三等分角” 是数学史上一个著名的问题， 但仅用尺规不可能 “三等分角”．下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法（如图）：将给定的锐角∠ AOB 置于直角坐标系中，边OB 在 x 轴上、边 OA 与函数xy1 的图象交于点 P，以 P 为圆心、以 2OP 为半径作弧交图象于点R．分别过点 P 和 R 作 x轴和 y 轴的平行线，两直线相交于点M ，连接 OM 得到∠ MOB，则∠ MOB=31∠AOB．要明白帕普斯的方法，请研究以下问题：（1）设)1,(aaP、)1,(bbR，求直线 OM 对应的函数表达式（用含ba, 的代数式表示）．（2）分别过点 P 和 R 作 y 轴和 x 轴的平行线，两直线相交于点Q．请说明 Q 点在直线 OM 上，并据此证明∠ MOB=31 ∠AOB．y x O P Q A B 3、（14 分）如图，在平面直角坐标系xOy中，矩形 OEFG的顶点 E 坐标为 (4 ，0) ，顶点 G坐标为 (0 ，2) ．将矩形 OEFG绕点 O逆时针旋转， 使点 F 落在轴的点 N处，得到矩形 OMNP，OM与 GF交于点 A．（1）判断△ OGA和△OMN是否相似，并说明理由；（2）求过点 A 的反比例函数解析式；（3）设（ 2）中的反比例函数图象交EF于点 B，求直线 AB的解析式；（4）请探索：求出的反比例函数的图象，是否经过矩形OEFG的对称中心，并说明理由．4、如图，在平面直角坐
