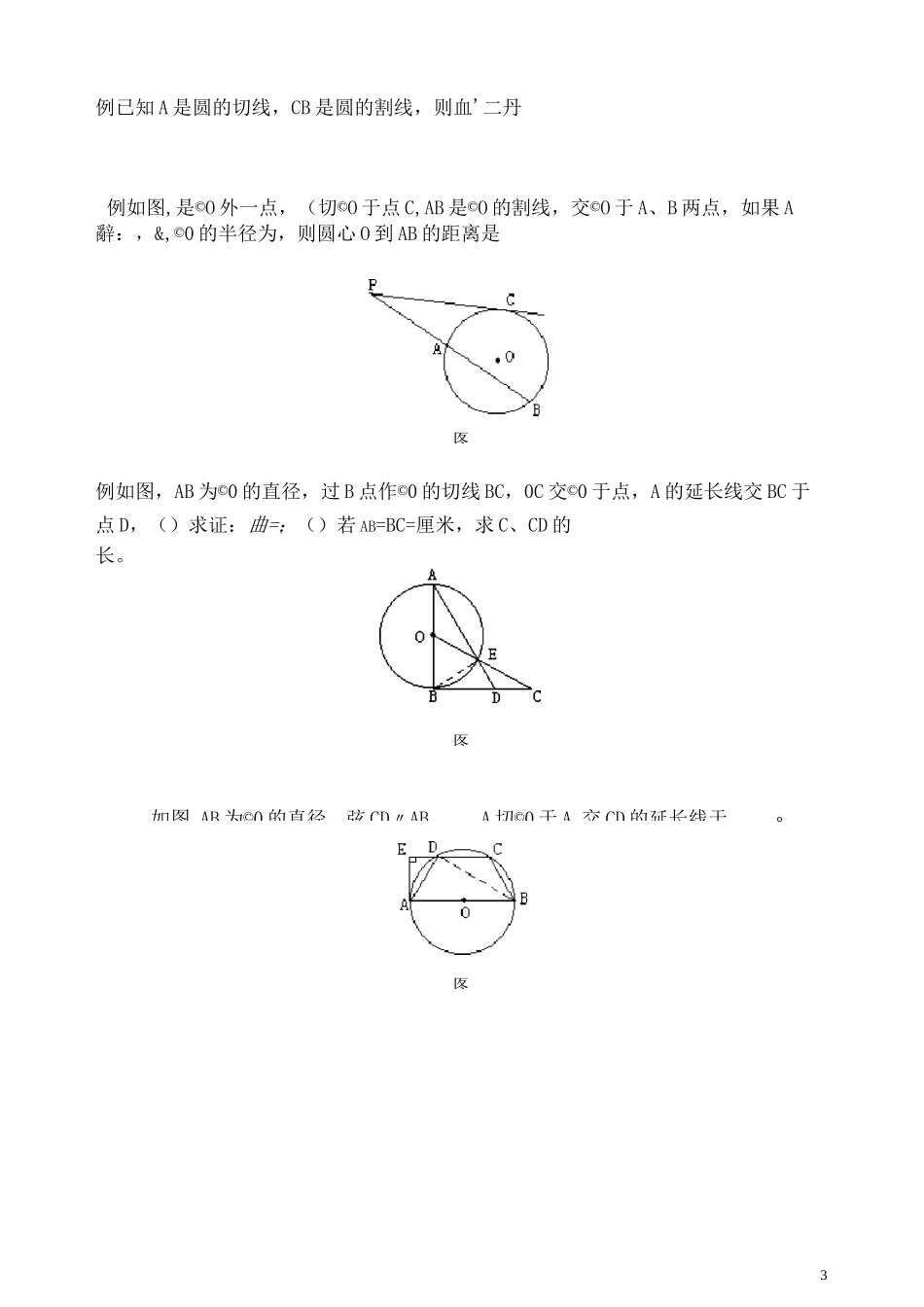
1直线 AB 切©O 于 P,PC、PD 为弦,图中几个弦切角呢?(四个)弦切角定理:弦切角等于其所夹的弧所对的圆周角。弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理。与圆有关的比例线定理图形已知结论OO 中,AB、CD 为弦,PA・PB交于 PPC・PD证法=连结 AC、BD,证:△APCs^DPB相交弦才■—定理的 A 推论 A(ProOO 中,AB 为直径,PC=PA・PBCD丄 AB 于 P用相交弦定切线长定理、弦切角定理、切割线定理、相交弦定理以及与圆有关的比例线段[学习目标]切线长概念切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。切线长定理对于切线长定理,应明确()若已知圆的两条切线相交,则切线长相等;()若已知两条切线平行,则圆上两个切点的连线为直径;()经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;()经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;()圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。弦切角:顶点在圆上,相交弦定理OO 中,T 切©O 于 T,PT=PA・PB 割线PB 交 OO 于 A连结 TA、TB,证:△PTBS^PATPB、PD 为 OO 的两条割 PA・PB=PC・PD 过 P 作 PT 切 OO 于 T,线,交 OO 于 A、C 用两次切割线定理圆幂定理OO 中,割线 PB 交 OOP'C・P'D=—延长 P'O 交 OO 于,于 A,CD 为弦 OP'延长 OP'交 OO 于,PA・PB=OP—用相交弦定理证;过 P 为OO 的半径作切线用切割线定理勾股定理证圆幂定理:过一定点 P 向 OO 作任一直线,交 OO 于两点,则自定点 P 到两交点的两条线段之积为常数 on(为圆半径),因为 0P2-R2叫做点对于 OO 的幂,所以将上述定理统称为圆幂定理。【典型例题】例如图,正方形 ABCD 的边长为,以 BC 为直径。在正方形内作半圆 O,过 A 作半圆切线,切点为,交 CD 于,求 D:A 的值。2例 OO 中的两条弦 AB 与 CD 相交于,若 A=,B=,CD=,那么 C=切割定理P图图c如图,AB 为©0 的直径,弦 CD〃AB,A 切©0 于 A,交 CD 的延长线于3例已知 A 是圆的切线,CB 是圆的割线,则血'二丹例如图,是©O 外一点,(切©O 于点 C,AB 是©O 的割线,交©O 于 A、B 两点,如果 A辭:...