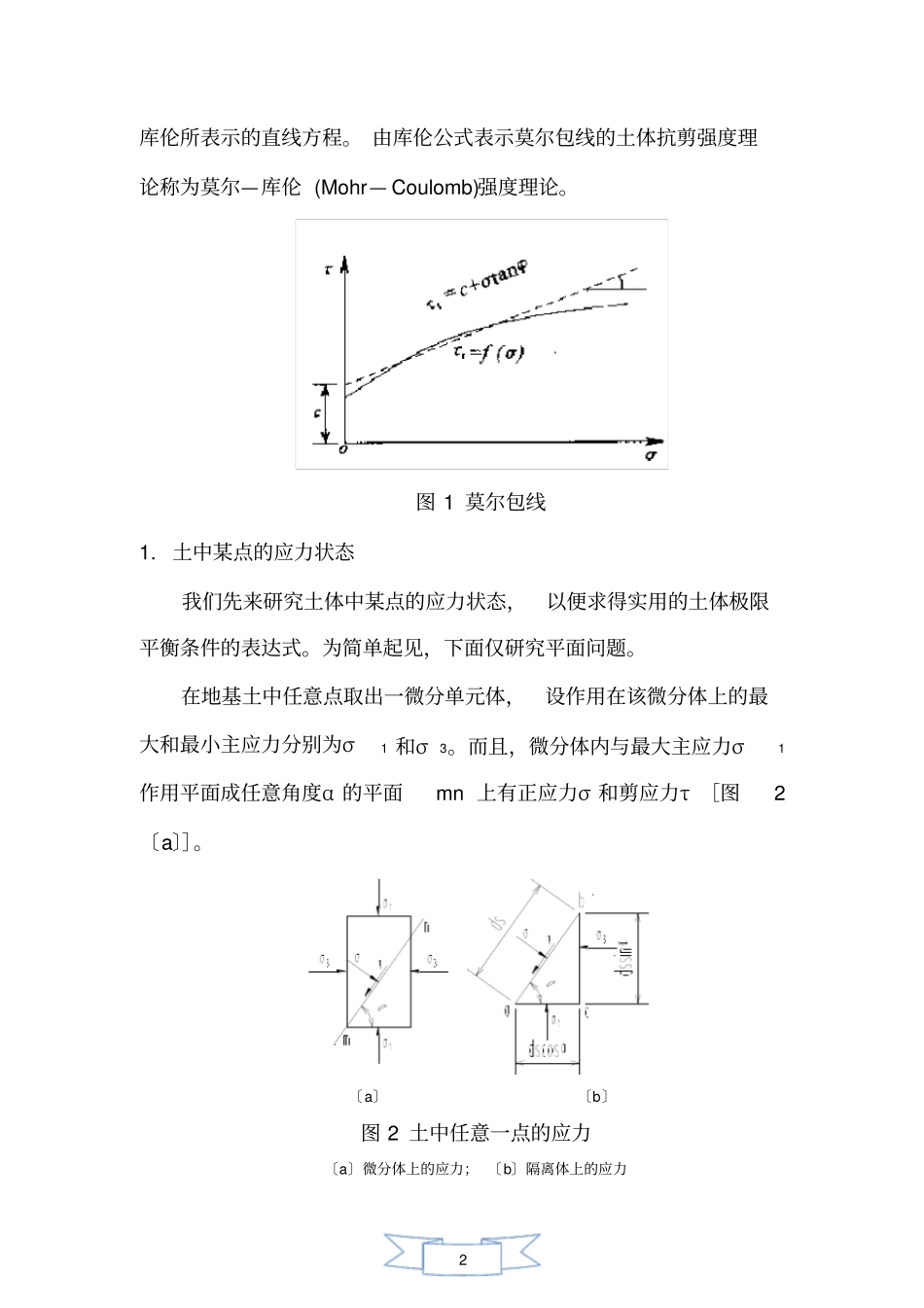
1 莫尔—库伦理论长期以来, 人们根据对材料破坏现象的分析,提出了各种不同的强度理论。 其中适用于土的强度理论有多种,不同的理论各有其优缺点。在土力学中被广泛采用的强度理论要推莫尔—库伦强度理论。1773 年,法国学者库伦 (Coulomb)根据砂土的试验结果,提出土的抗剪强度τf 在应力变化不大的范围内,可表示为剪切滑动面上法向应力σ 的线性函数。即后来库伦又根据粘性土的试验结果,提出更为普遍的抗剪强度公式: 1936 年,太沙基 (Terzaghi)提出了有效应力原理。根据有效应力原理,土中总应力等于有效应力与孔隙水压力之和,只有有效应力的变化才会引起强度的变化。因此,土的抗剪强度可表示为剪切破坏面上法向有效应σ’的函数。上述库仑公式应改写为1910 年莫尔 (Mohr) 提出材料产生剪切破坏时, 破坏面上的是该面上法向应力的函数,即该函数在直角坐标系中是一条曲线,如图 1 所示,通常称为莫尔包线。土的莫尔包线多数情况下可近似地用直线表示,其表达式就是2 库伦所表示的直线方程。 由库伦公式表示莫尔包线的土体抗剪强度理论称为莫尔—库伦 (Mohr— Coulomb)强度理论。图 1 莫尔包线1. 土中某点的应力状态我们先来研究土体中某点的应力状态,以便求得实用的土体极限平衡条件的表达式。为简单起见,下面仅研究平面问题。在地基土中任意点取出一微分单元体,设作用在该微分体上的最大和最小主应力分别为σ1 和σ3。而且,微分体内与最大主应力σ1作用平面成任意角度α 的平面mn 上有正应力σ 和剪应力τ [图2〔a〕]。〔a〕〔b〕图 2 土中任意一点的应力〔a〕微分体上的应力; 〔b〕隔离体上的应力3 为了建立σ、τ 与σ1 和σ3 之间的关系,取微分三角形斜面体abc 为隔离体 [图 2〔b〕]。将各个应力分别在水平方向和垂直方向上投影根据静力平衡条件得310,sin1.0sin1.0cos1.00( )0,cos1.0cos1.0sin1.00( )xdsdsdsaydsdsdsb联立求解以上方程 (a) 、(b) ,即得平面 mn上的应力13131311()()cos 222(1)1 ()sin 22由以上两式可知,在σ1 和σ3 已知的情况下,斜截面mn 上的法向应力σ 和剪应力τ 仅与斜截面倾角α 有关。由式〔1〕得上式表示圆心为〔〕、半径为关的莫尔圆。莫尔圆上任一点代表与大主应力σ1 作用面成α 角的斜面,其纵坐标代表该面上的法向应力,横坐标代表该面上的剪应力。在直角坐标系中〔图3〕以σ 为横坐标轴.以τ 为纵坐标轴,按图 3 用莫尔应力圆求...