弹性力学平面应力平面应变问题VIP免费

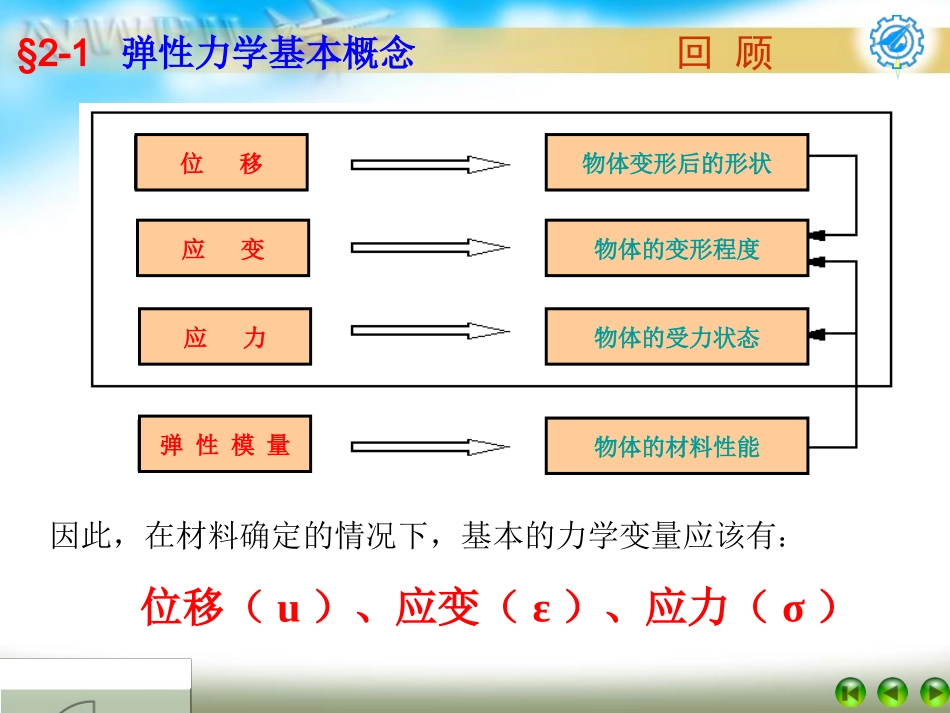
因此，在材料确定的情况下，基本的力学变量应该有：位移（u）、应变（ε）、应力（σ）量回顾§2-1弹性力学基本概念位移应变应力弹性模量物体的材料性能物体的受力状态物体的变形程度物体变形后的形状dydxdz弹性力学目的：对弹性体中的位移、应力、应变进行定义和表达，进而建立平衡方程、几何方程和材料物理方程研究的基本技巧采用微小体积元dxdydz的分析方法（针对任意变形体）回顾弹性体的基本假设为突出所处理的问题的实质，并使问题简单化和抽象化，在弹性力学中，特提出以下几个基本假定。(1)物质连续性假定：物质无空隙，可用连续函数来描述；(2)物质均匀性假定：物体内各个位置的物质具有相同特性；(3)物质(力学)特性各向同性假定：物体内同一位置的物质在各个方向上具有相同特性；(4)线性弹性假定：物体的变形与外来作用力的关系是线性的，外力去除后，物体可恢复原状；(5)小变形假定：物体变形远小于物体的几何尺寸。以上基本假定将作为问题简化的出发点。回顾a’bb’aa’dd’cc’xyxyyxyxyzyzzyzyzxzxxzxz回顾§2-2弹性力学基本方程由力平衡条件0X有0Xdxdydzdxdydxdydzzdxdzdxdzdyydydzdydzdxxzxzxzxyxyxyxxxx化简得到0Xzyxzxyxx0Y0Yzyxzyyxy0Z0Zzyxzyzxz1.平衡微分方程回顾平衡微分方程的矩阵形式为0bσ其中，是微分算子xyzzxyzyx000000000式中，b是体积力向量，T][ZYXb回顾二维问题：平衡微分方程0Xyxyxx0Yyxyxy回顾2.几何方程：位移-应变的关系B1A1θ1θ2回顾xuxyuxvxyyvyzvywyzzwzxwzuzx六个应变分量与三个位移分量间的全部关系式：回顾2.几何方程：位移-应变的关系几何方程式的矩阵形式为uεt为微分算子t其中的转置T000000000xzyzxyzyxt回顾由简单的轴向拉伸试验可知，在单向应力状态下，处于弹性阶段时，应力应变呈线性关系，即σx=Eεx这就是虎克定律。弹塑性范围斜率,E弹性范围应力Y应变3.物理方程：应力-应变的关系（Hooke‘sLaw）工程上，一般将应变与应力间的关系表示为zyxxE1xzyyE1yxzzE1xyxyG1yzyzG1zxzxG1称它们为物理方程（广义虎克定律）。zyxxE112111zyxyE112111zyxzE112111xyxyE12yzyzE12zxzxE12若令TzxyzxyzyxTzxyzxyzyx代表应变列阵和应力列阵，则应力-应变关系可写成矩阵形式D其中1221000001221000012210001111112111称对ED称为弹性矩阵，由弹性常数E和μ决定。回顾4.应力边界条件弹性体在应力边界上单位面积的面力为、、。设边界外法线的方向余弦为，则边界上弹性体的应力边界条件可表示为XYZtzyxnnn、、zzzyyzxxyzzyyyxxxzzxyyxxnnnZnnnYnnnX其矩阵表达式为nσt(在上)t其中，面积力向量，方向余弦矩阵为T][ZYXtxyzzxyzyxnn0n000nn0n0n0n00nn5.位移边界条件回顾已知位移边界上弹性体的位移为，则有uwvu、、uuvvwwu(在上)用矩阵形式表示为：uuu(...