杆件横截面上的应力VIP免费

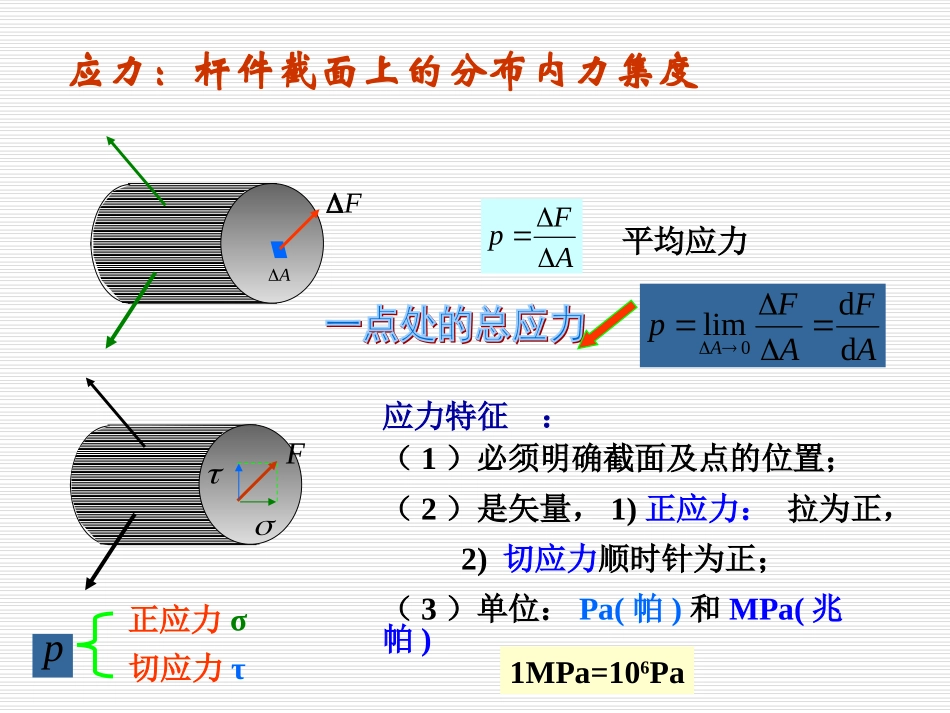
杆件横截面上的应力第七章第一节基本概念第二节轴向拉压杆的应力应力应变胡克定律横截面上的应力斜截面上的应力应力：杆件截面上的分布内力集度AFp平均应力AFAFpAddlim0p正应力σ切应力τ应力特征：（1）必须明确截面及点的位置；（2）是矢量，1)正应力：拉为正，2)切应力顺时针为正；（3）单位：Pa(帕)和MPa(兆帕)1MPa=106PaFAF杆原长为l，直径为d。受一对轴向拉力F的作用，发生变形。变形后杆长为l1，直径为d1。其中：拉应变为正，压应变为负。lllll1轴向(纵向)应变：研究一点的线应变：取单元体积为Δx×Δy×Δzxxxxxxddlim0该点沿x轴方向的线应变为：x方向原长为Δx，变形后其长度改变量为Δδx应变Oxyzx横向应变：ddddd1'胡克定律实验表明，在比例极限内，杆的轴向变形Δl与外力F及杆长l成正比，与横截面积A成反比。即：AFll引入比例常数E，有：EAlFEAFllN----胡克定律其中：E----弹性模量，单位为Pa;EA----杆的抗拉（压）刚度。胡克定律的另一形式：E实验表明，横向应变与纵向应变之比为一常数ν----称为横向变形系数（泊松比）''||||E'GG------切变模量FF11221122假设：①平面假设②横截面上各点处仅存在正应力并沿截面均匀分布。AFAFN拉应力为正，压应力为负。对于等直杆当有多段轴力时，最大轴力所对应的截面-----危险截面。危险截面上的正应力----最大工作应力AFmax,NmaxFNFFNF拉压杆横截面上的应力FN:横截面上的轴力A：横截面的面积横截面----是指垂直杆轴线方向的截面；斜截面----是指任意方位的截面。FFFNFppcoscos0AFp2coscosp2sin2sin0p①全应力：②正应力：③切应力：1）α=00时，σmax＝σ2）α＝450时，τmax=σ/2拉压杆斜截面上的应力试计算图示杆件1-1、2-2、和3-3截面上正应力.已知横截面面积A=2×103mm220KN20KN40KN40KN332211例题例题20kN40kNMPa1011022MPa2033试求图示结构AB杆横截面上的正应力。已知F=30KN，A=400mm2FDBCAaaa例题例题FNAB02aFaFABNFFNAB2MPaAFNAB150图示直杆，其抗拉刚度为EA，试求杆件的轴向变形△L，B点的位移δB和C点的位移δCFBCALL例题例题FEAFLLABBEAFLBC梁弯曲时横截面上的正应力与切应力，分别称为弯曲正应力与弯曲切应力。MSFMFSFSM第四节第四节纯弯曲时梁横截面上的正应力纯弯曲：梁受力弯曲后，如其横截面上只有弯矩而无剪力，这种弯曲称为纯弯曲。纯弯曲时梁横截面上的正应力aFACaFBDFFFa实验现象：1、变形前互相平行的纵向直线、变形后变成弧线，且凹边纤维缩短、凸边纤维伸长。2、变形前垂直于纵向线的横向线,变形后仍为直线，且仍与弯曲了的纵向线正交，但两条横向线间相对转动了一个角度。中性轴：中性层与横截面的交线称为中性轴。平面假设：变形前杆件的横截面变形后仍为平面。mmnnFF中性层中性轴m1onn2omdxmmnnozyoddxmmnnFFydddyyEEyMM中性轴yzdAAdANFAdAzyMAdAyzMAydAE0AzydAE0AdAyE2ZEIZZEIM1zzIyMzzIyMMZ:横截面上的弯矩y:到中性轴的距离IZ:截面对中性轴的惯性矩dxmmnnozyoMM中性轴yzdAzWxMmaxM中性轴MzzWMmax横截面上正应力的画法：MminmaxMminmax①线弹性范围—正应力小于比例极限p；②精确适用于纯弯曲梁；③对于横力弯曲的细长梁(跨度与截面高度比L/h>5)，上述公式的误差不大，但公式中的M应为所研究截面上的弯矩，即为截面位置的函数。zzEIxMxIyxM)()(1)(，公式适用范围：三种典型截面对中性轴的惯性矩IbhZ312IdZ464IDdDZ()()444464641CL8TU6,WbhZ26,WdZ332WDZ34321()长为l的矩形截面悬臂梁，在自由端作用一集中力F，已知b＝120mm，h＝180mm、l＝2m，F＝1.6kN，试求B截面上a、b、c各点的正应力。2lF2lABCbh6h2habcFLFLMB...