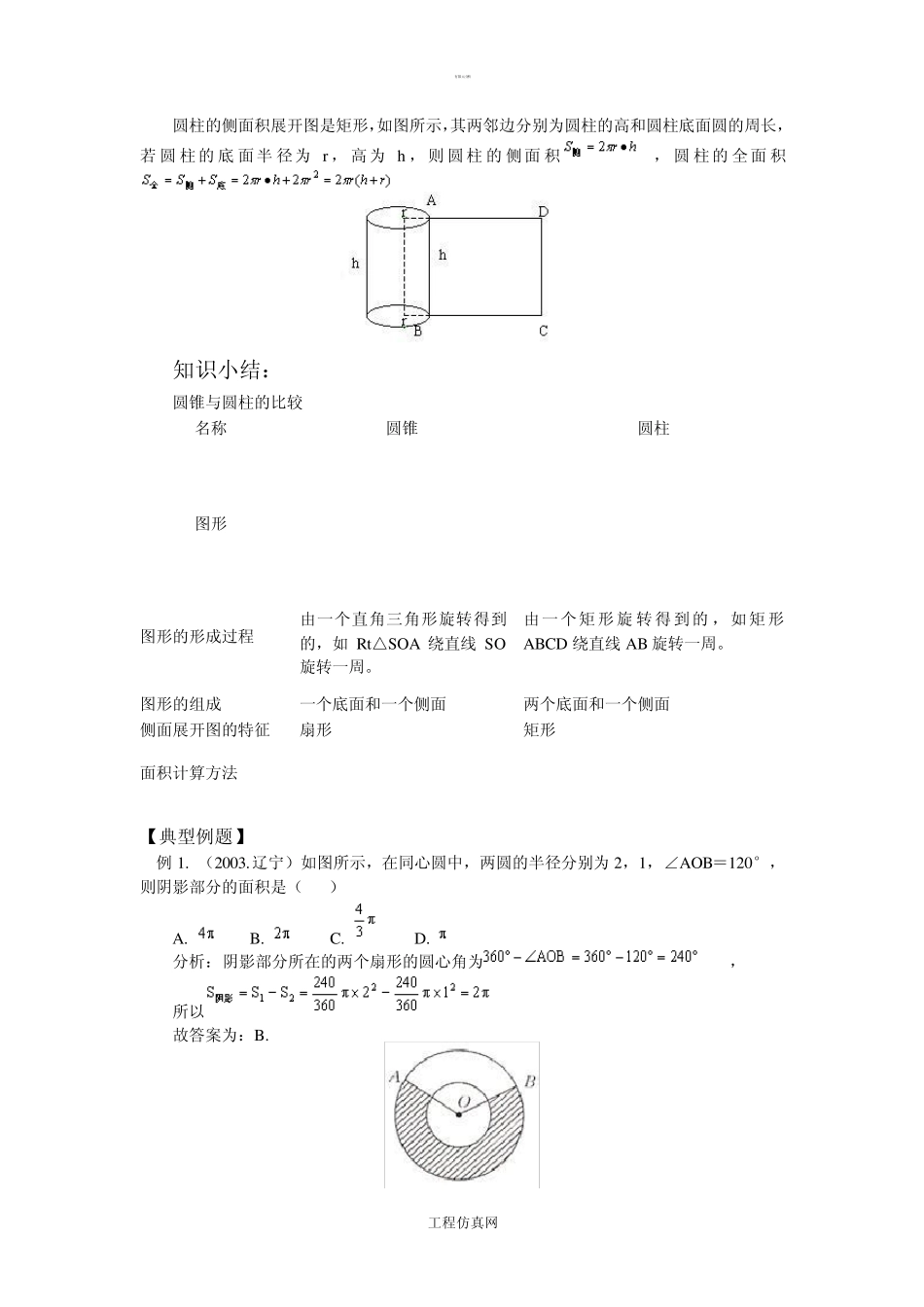
有限元分析 工程仿真网 弧形、扇形公式解说和运用 知识点1 、弧长公式 因为360°的圆心角所对的弧长就是圆周长C=2R,所以 1°的圆心角所对的弧长是,于是可得半径为R 的圆中,n°的圆心角所对的弧长l 的计算公式:, 说明:(1)在弧长公式中,n表示 1°的圆心角的倍数,n和180 都不带单位“度”,例如,圆的半径 R=10,计算 20°的圆心角所对的弧长l 时,不要错写成。 (2)在弧长公式中,已知l,n,R 中的任意两个量,都可以求出第三个量。 知识点2 、扇形的面积 如图所示,阴影部分的面积就是半径为R,圆心角为n°的扇形面积,显然扇形的面积是它所在圆的面积的一部分,因为圆心角是 360°的扇形面积等于圆面积,所以圆心角为1°的扇形面积是,由此得圆心角为n°的扇形面积的计算公式是。 又因为扇形的弧长 ,扇形面积,所以又得到扇形面积的另一个计算公式:。 知识点3 、弓形的面积 (1)弓形的定义:由弦及其所对的弧(包括劣弧、优弧、半圆)组成的图形叫做弓形。 (2)弓形的周长=弦长+弧长 (3)弓形的面积 如图所示,每个圆中的阴影部分的面积都是一个弓形的面积,从图中可以看出,只要把扇形OAmB 的面积和△AOB 的面积计算出来,就可以得到弓形AmB 的面积。 当弓形所含的弧是劣弧时,如图 1 所示, 当弓形所含的弧是优弧时,如图 2 所示, 当弓形所含的弧是半圆时,如图 3 所示, 例:如图所示,⊙O 的半径为2,∠ABC=45°,则图中阴影部分的面积是 ( )(结果用表示) 有限元分析 工程仿真网 分析:由图可知由圆周角定理可知∠ABC=∠AOC,所以∠AOC=2∠ABC=90°,所以△OAC 是直角三角形,所以 , 所以 注意:(1)圆周长、弧长、圆面积、扇形面积的计算公式。 圆周长 弧长 圆面积 扇形面积 公 式 (2)扇形与弓形的联系与区别 (2)扇形与弓形的联系与区别 图 示 面 积 知识点 4 、圆锥的侧面积 圆锥的侧面展开图是一个扇形,如图所示,设圆锥的母线长为 l,底面圆的半径为 r,那么这个扇形的半径为 l,扇形的弧长为 2,圆锥的侧面积,圆锥的全面积 说明:(1)圆锥的侧面积与底面积之和称为圆锥的全面积。 (2)研究有关圆锥的侧面积和全面积的计算问题,关键是理解圆锥的侧面积公式,并明确圆锥全面积与侧面积之间的关系。 知识点 5 、圆柱的侧面积 有限元分析 工程仿真网 圆柱的侧面积展开图是矩形,如图所示,其两邻边分别为圆柱的高和...