数字信号处理(姚天任江太辉第三版)课后习题答案

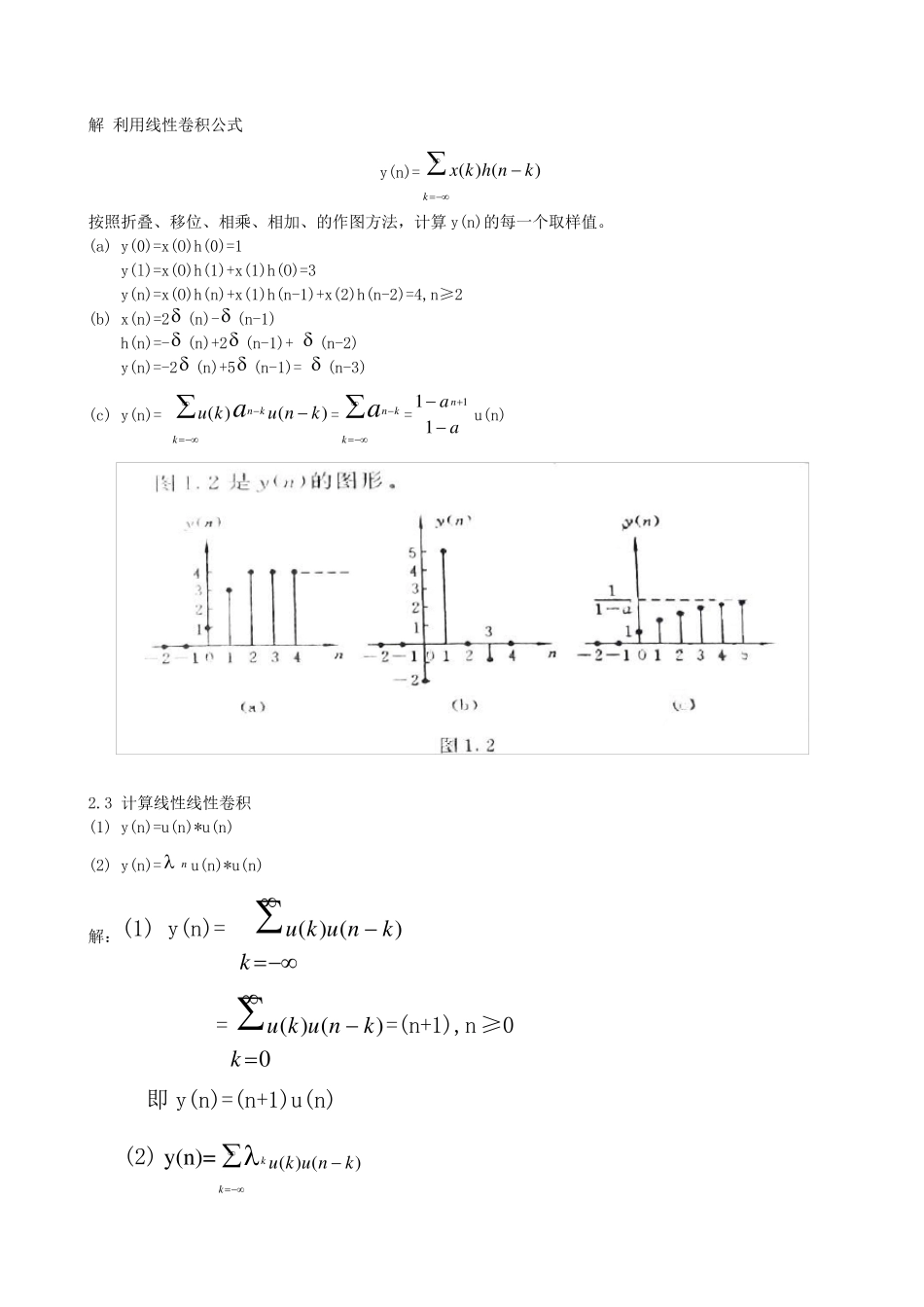
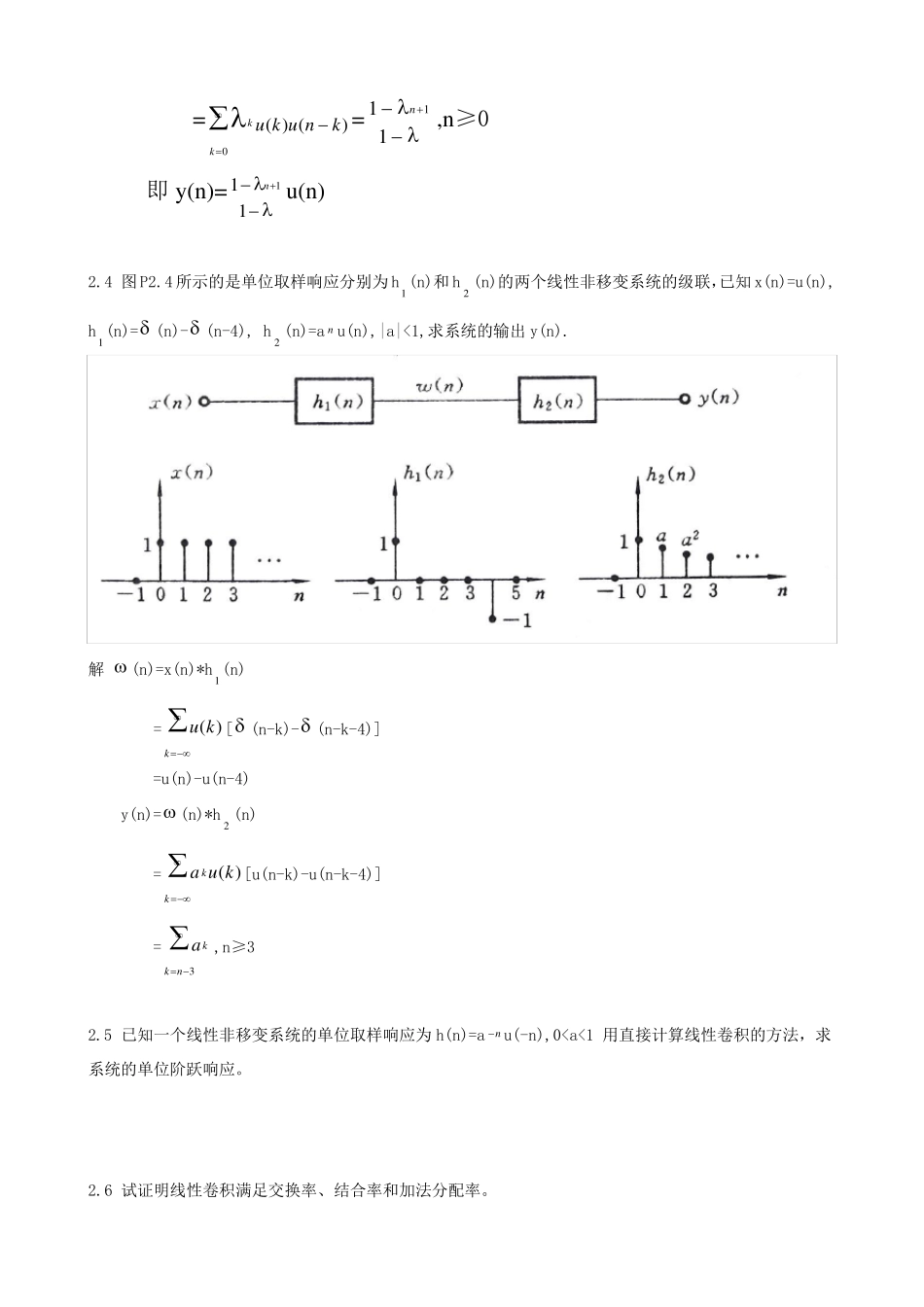
第二章 2.1 判断下列序列是否是周期序列。若是，请确定它的最小周期。 （1）x(n)=Acos(685n) （2）x(n)=)8(ne j （3）x(n)=Asin(343n) 解 (1)对照正弦型序列的一般公式x(n)=Acos( n)，得出85。因此 5162是有理数，所以是周期序列。最小周期等于N=)5(16516取kk 。 （2）对照复指数序列的一般公式x(n)=exp[j]n,得出81。因此 162是无理数，所以不是周期序列。 （3）对照正弦型序列的一般公式x(n)=Acos( n)，又x(n)=Asin(343n)＝Acos(2343n)＝Acos(6143n) ，得出43。因此382是有理数，所以是周期序列。最小周期等于N=)3(838取kk  2.2 在图2.2 中，x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n)，并画出y(n)的图形。 (a)1111 (b) (c)111110 0 0 0 0 0 -1-1-1-1-1-1-1-1222222 3 3 3 3 3444………nnnnnnx(n)x(n)x(n)h(n)h(n)h(n)21u(n)u(n)u(n)an===22 解 利用线性卷积公式 y(n)= kknhkx)()( 按照折叠、移位、相乘、相加、的作图方法，计算y(n)的每一个取样值。 (a) y(0)=x(O)h(0)=1 y(l)=x(O)h(1)+x(1)h(O)=3 y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n≥2 (b) x(n)=2 (n)- (n-1) h(n)=- (n)+2 (n-1)+  (n-2) y(n)=-2 (n)+5 (n-1)=  (n-3) (c) y(n)= kknknukua)()(= kkna=aa n111u(n) 2.3 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)= n u(n)*u(n) 解：(1) y(n)= kknuku)()( = 0)()(kknuku=(n+1),n≥0 即 y(n)=(n+1)u(n) (2) y(n)= kkknuku)()( =0)()(kkknuku=111n,n≥0 即 y(n)=111n u(n) 2.4 图 P2.4 所示的是单位取样响应分别为 h1(n)和 h2 (n)的两个线性非移变系统的级联，已知 x(n)=u(n), h1(n)= (n)- (n-4), h2 (n)=a n u(n),|a|<1,求系统的输出 y(n). 解  (n)=x(n)*h1(n) = kku)([ (n-k)- (n-k-4)] =u(n)-u(n-4) y(n)= (n)*h2 (n) = kkkua)([u(n-k)-u(n-k-4)] = 3nkka,n≥3 2.5 已知一个线性非移变系统的单位取样响应为 h(n)=an u(-n),0