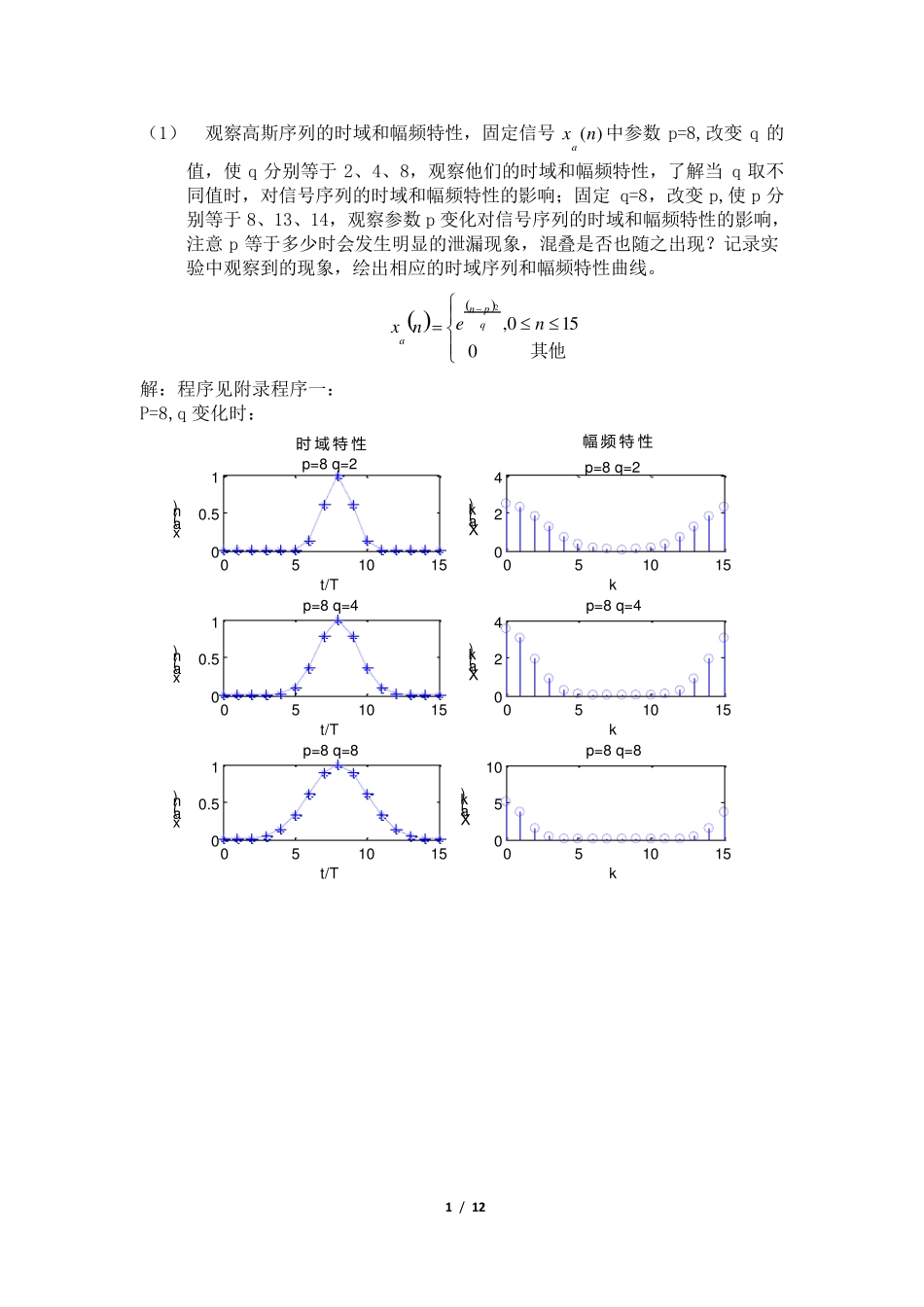
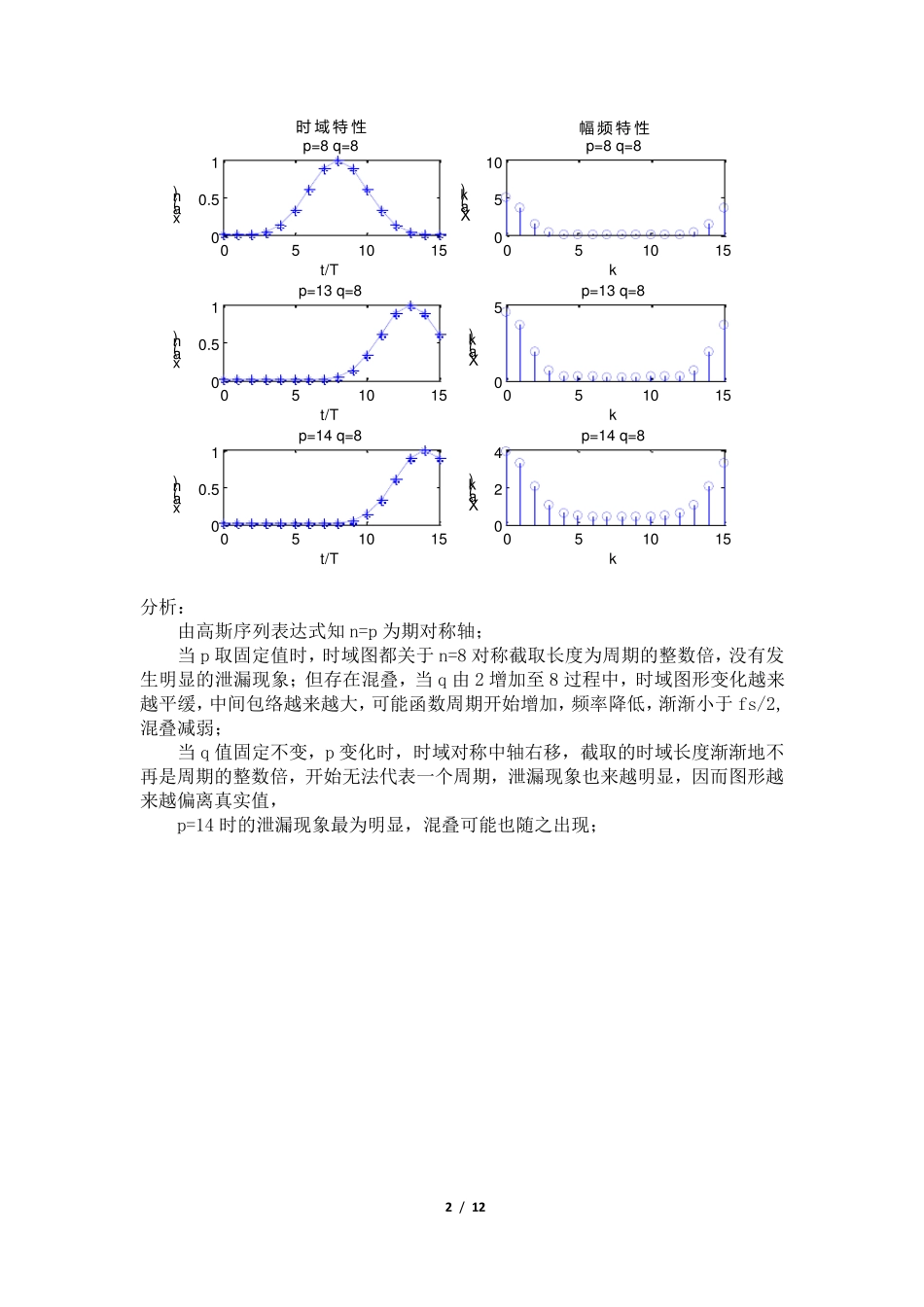
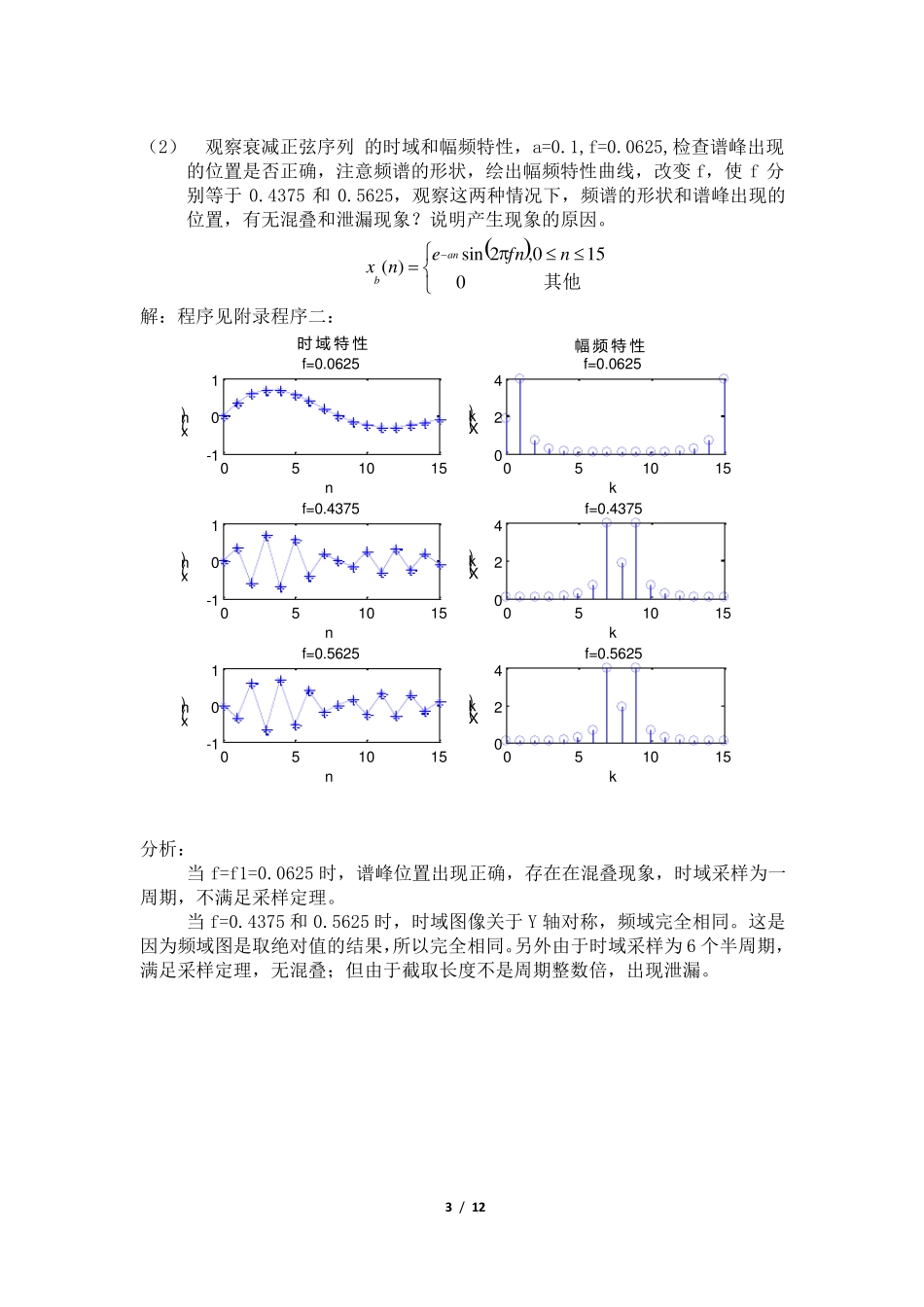
1 / 12 (1) 观察高斯序列的时域和幅频特性,固定信号)(nxa中参数p=8,改变q 的值,使q 分别等于2、4、8,观察他们的时域和幅频特性,了解当 q 取不同值时,对信号序列的时域和幅频特性的影响;固定q=8,改变p,使p 分别等于8、13、14,观察参数p 变化对信号序列的时域和幅频特性的影响,注意 p 等于多少时会发生明显的泄漏现象,混叠是否也随之出现?记录实验中观察到的现象,绘出相应的时域序列和幅频特性曲线。 其他01 50,2nenxqpna 解:程序见附录程序一: P=8,q 变化时: 05101500.51t/Txa(n)p=8 q=2051015024kXa(k)p=8 q=205101500.51t/Txa(n)p=8 q=4051015024kXa(k)p=8 q=405101500.51t/Txa(n)p=8 q=80510150510kXa(k)p=8 q=8幅 频 特 性时 域 特 性 2 / 12 05101500.51t/Txa(n)p=8 q=80510150510kXa(k)p=8 q=805101500.51t/Txa(n)p=13 q=805101505kXa(k)p=13 q=805101500.51t/Txa(n)p=14 q=8051015024kXa(k)p=14 q=8时 域 特 性幅 频 特 性 分析: 由高斯序列表达式知n=p 为期对称轴; 当p 取固定值时,时域图都关于n=8 对称截取长度为周期的整数倍,没有发生明显的泄漏现象;但存在混叠,当q 由2 增加至8 过程中,时域图形变化越来越平缓,中间包络越来越大,可能函数周期开始增加,频率降低,渐渐小于fs/2,混叠减弱; 当q 值固定不变,p 变化时,时域对称中轴右移,截取的时域长度渐渐地不再是周期的整数倍,开始无法代表一个周期,泄漏现象也来越明显,因而图形越来越偏离真实值, p=14 时的泄漏现象最为明显,混叠可能也随之出现; 3 / 12 (2) 观察衰减正弦序列 的时域和幅频特性,a=0.1,f=0.0625,检查谱峰出现的位置是否正确,注意频谱的形状,绘出幅频特性曲线,改变f,使f 分别等于0.4375 和0.5625,观察这两种情况下,频谱的形状和谱峰出现的位置,有无混叠和泄漏现象?说明产生现象的原因。 其他0150,2sin)(nfnenxanb 解:程序见附录程序二: 051015-101nx(n)f=0.0625051015024kX(k)f=0.0625051015-101nx(n)f=0.4375051015024kX(k)f=0.4375051015-101nx(n)f=0.5625051015024kX(k)f=0.5625幅 频 特 性时 域 特 性 分析: 当 f=f1=0.0625 时,谱峰位置出现正确,存在在混叠现象,时域采样为一周期,不满足采样定理。 当 f=0.4375 和0.5625 时,时域图像关于Y 轴对称,频域完全相同。这是...