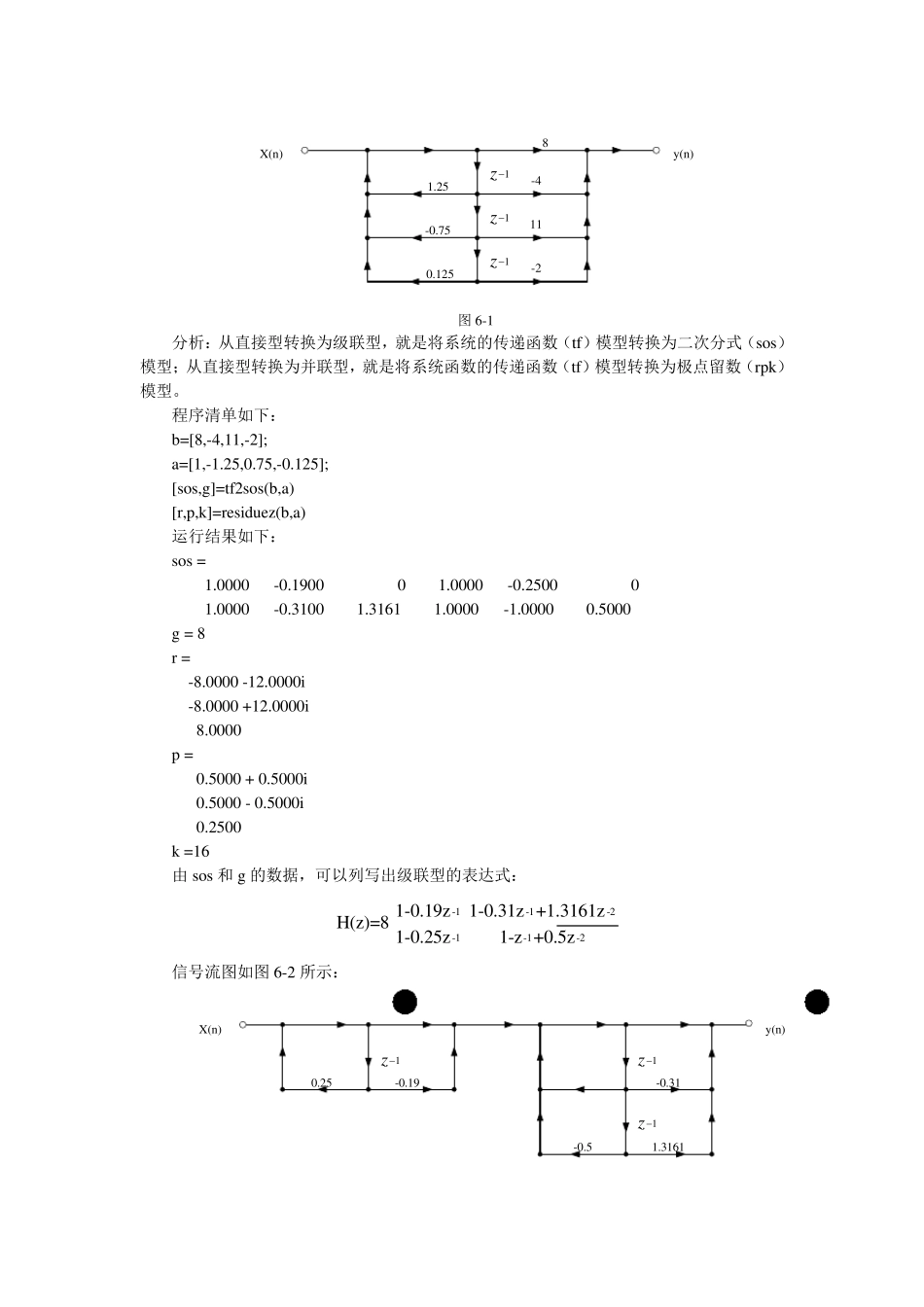
实验 6 数字滤波器的网络结构 一、实验目的: 1、加深对数字滤波器分类与结构的了解。 2、明确数字滤波器的基本结构及其相互间的转换方法。 3、掌握用 MATLAB 语言进行数字滤波器结构间相互转换的子函数及程序编写方法。 二、实验原理: 1、数字滤波器的分类 离散 LSI 系统对信号的响应过程实际上就是对信号进行滤波的过程。因此,离散 LSI系统又称为数字滤波器。 数字滤波器从滤波功能上可以分为低通、高通、带通、带阻以及全通滤波器;根据单位脉冲响应的特性,又可以分为有限长单位脉冲响应滤波器(FIR)和无限长单位脉冲响应滤波器(IIR)。 一个离散 LSI 系统可以用系统函数来表示: M-m-1-2-mmm=0012mN-1-2-k-k12kkk=1b zb +b z +b z ++b zY(z)b(z)H(z)====X(z)a(z)1+a z +a z ++a z1+a z 也可以用差分方程来表示: NMkmk=1m=0y(n)+a y(n-k)=b x(n-m) 以上两个公式中,当 ak 至少有一个不为 0 时,则在有限 Z 平面上存在极点,表达的是以一个 IIR 数字滤波器;当 ak 全都为 0 时,系统不存在极点,表达的是一个 FIR 数字滤波器。FIR 数字滤波器可以看成是 IIR 数字滤波器的 ak 全都为 0 时的一个特例。 IIR 数字滤波器的基本结构分为直接Ⅰ型、直接Ⅱ型、直接Ⅲ型、级联型和并联型。 FIR 数字滤波器的基本结构分为横截型(又称直接型或卷积型)、级联型、线性相位型及频率采样型等。本实验对线性相位型及频率采样型不做讨论,见实验 10、12。 另外,滤波器的一种新型结构——格型结构也逐步投入应用,有全零点 FIR 系统格型结构、全极点 IIR 系统格型结构以及全零极点 IIR 系统格型结构。 2、IIR 数字滤波器的基本结构与实现 (1)直接型与级联型、并联型的转换 例 6-1 已知一个系统的传递函数为 -1-2-3-1-2-38-4z +11z -2zH(z)= 1-1.25z +0.75z -0.125z 将其从直接型(其信号流图如图 6-1 所示)转换为级联型和并联型。 X(n)y(n)81.25-0.750.125-411-21z1z1z 图6-1 分析:从直接型转换为级联型,就是将系统的传递函数(tf)模型转换为二次分式(sos)模型;从直接型转换为并联型,就是将系统函数的传递函数(tf)模型转换为极点留数(rpk)模型。 程序清单如下: b=[8,-4,11,-2]; a=[1,-1.25,0.75,-0.125]; [sos,g]=tf2sos(b,a) [r,p,k]=residuez(b,a) 运行结果如下: sos = 1.0000 -0.1900 0 1.0000 -0.2500 0 1.0...