数字信号处理实验四

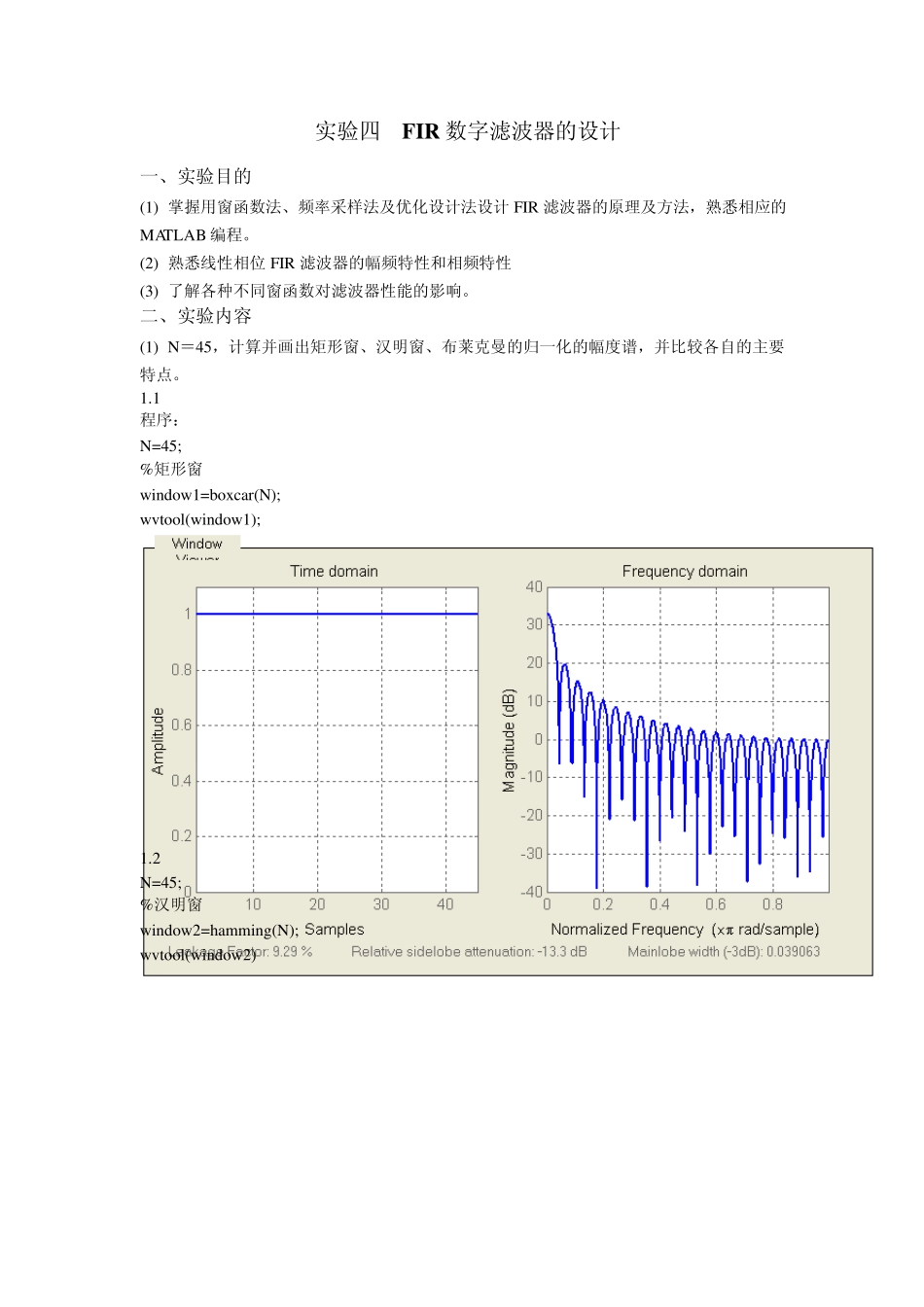
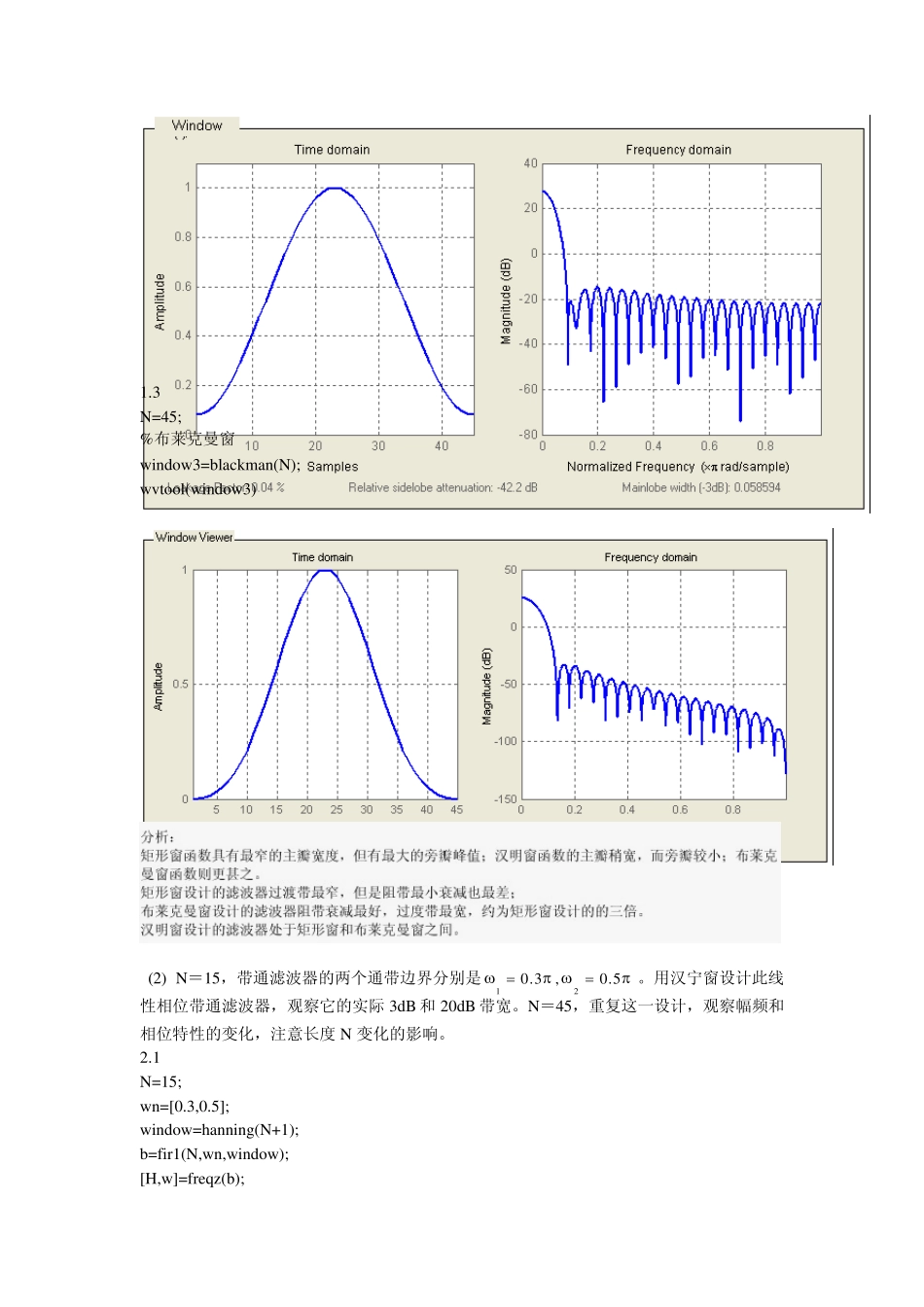
实验四 FIR 数字滤波器的设计 一、实验目的 (1) 掌握用窗函数法、频率采样法及优化设计法设计FIR 滤波器的原理及方法，熟悉相应的MATLAB 编程。 (2) 熟悉线性相位 FIR 滤波器的幅频特性和相频特性 (3) 了解各种不同窗函数对滤波器性能的影响。 二、实验内容 (1) N＝45，计算并画出矩形窗、汉明窗、布莱克曼的归一化的幅度谱，并比较各自的主要特点。 1.1 程序： N=45; %矩形窗 window1=boxcar(N); wvtool(window1); 1.2 N=45; %汉明窗 window2=hamming(N); wvtool(window2) 1.3 N=45; %布莱克曼窗 window3=blackman(N); wvtool(window3) (2) N＝15，带通滤波器的两个通带边界分别是120.3,0.5 。用汉宁窗设计此线性相位带通滤波器，观察它的实际 3dB 和 20dB 带宽。N＝45，重复这一设计，观察幅频和相位特性的变化，注意长度 N 变化的影响。 2.1 N=15; wn=[0.3,0.5]; window=hanning(N+1); b=fir1(N,wn,window); [H,w]=freqz(b); plot(w/pi,20*log10(abs(H))) figure plot(w/pi,angle(H)) 2.2 N=45; wn=[0.3,0.5]; window=hanning(N+1); b=fir1(N,wn,window); [H,w]=freqz(b); plot(w/pi,20*log10(abs(H))) figure plot(w/pi,angle(H)) (3) 分别改用矩形窗和布莱克曼窗，设计(2)中的带通滤波器，观察并记录窗函数对滤波器幅频特性的影响，比较三种窗的特点。 3.1 矩形窗： N=15 wn=[0.3,0.5] b=fir1(N,wn,boxcar(N+1)) [H,w]=freqz(b,1,512) plot(w/pi,20*log10(abs(H))) xlabel('normalized frequency');ylabel('magnitude') title('magnitude response') figure plot(w/pi,angle(H)) xlabel('normalized frequency');ylabel('phase') title('phase response') 布莱克曼窗： N=15 wn=[0.3,0.5] window=blackman(N+1); b=fir1(N,wn,window); [H,w]=freqz(b); plot(w/pi,20*log10(abs(H))) xlabel('normalized frequency');ylabel('magnitude') title('magnitude response') figure plot(w/pi,angle(H)) xlabel('normalized frequency');ylabel('phase') (4) 用凯塞窗设计一专用线性相位滤波器，N＝40，|() |jdHe 如实验图四图，当4 6 10 、、时，分别设计、比较它们的幅频和相频特性，注意  取不同值时的影响。 N=40; %beta=4 for n=1:3 if n==1 beta=4; elseif n==2 beta=6; else beta=10; end; w=kais...