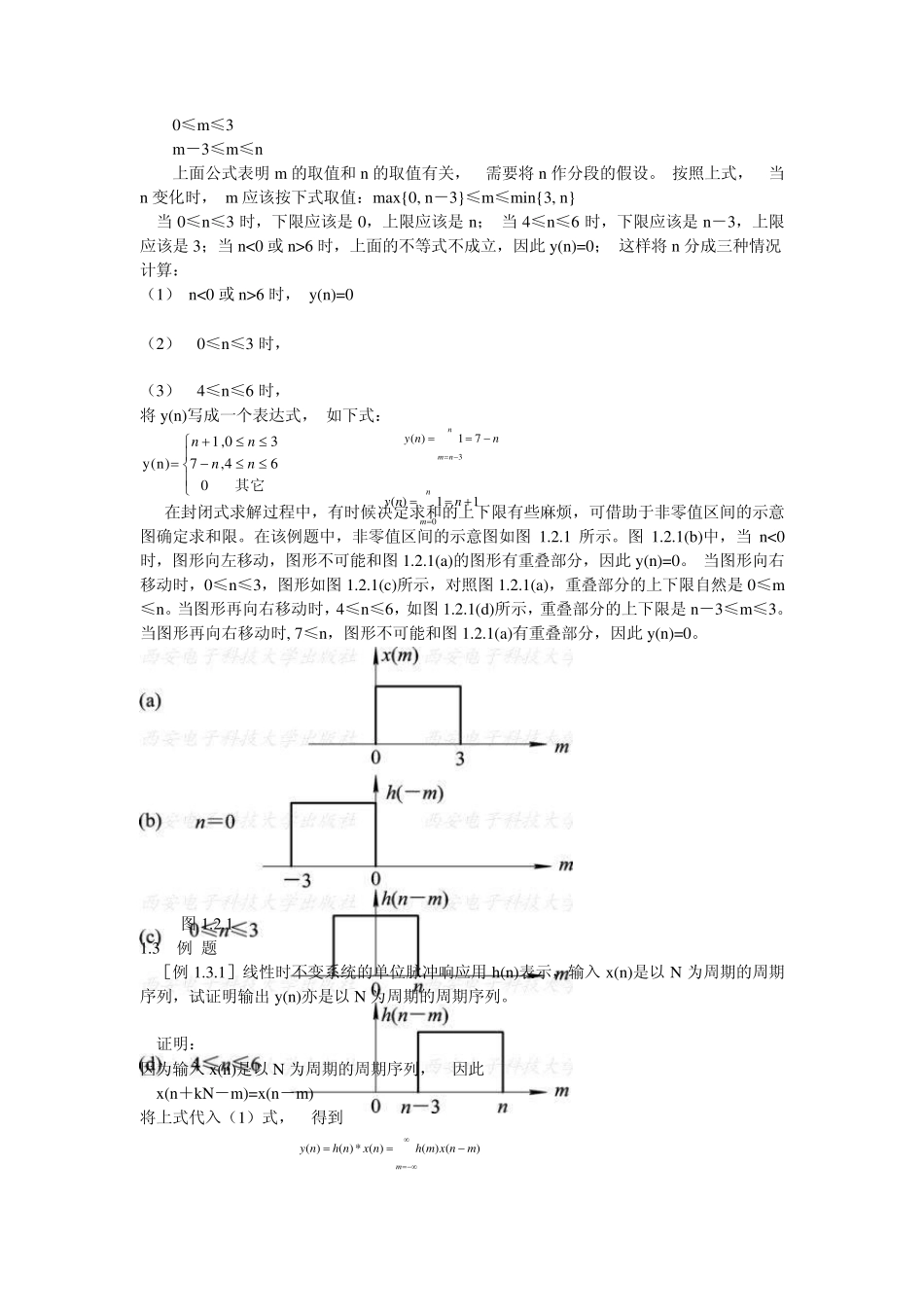
第 1 章 时域离散信号和时域离散系统 1.1.2 重要公式 (1) mnhnxmnhmxny)(*)()()()( 这是一个线性卷积公式, 注意公式中是在-∞~∞之间对 m 求和。 如果公式中 x(n)和 h(n)分别是系统的输入和单位脉冲响应, y(n)是系统输出, 则该式说明系统的输入、 输出和单位脉冲响应之间服从线性卷积关系。 (2)x(n)=x(n)*δ (n) 该式说明任何序列与δ (n)的线性卷积等于原序列。 x(n-n0)=x(n)*δ (n-n0) (3)kankXTX)jj(1)j(ˆs 这是关于采样定理的重要公式, 根据该公式要求对信号的采样频率要大于等于该信号的最高频率的两倍以上, 才能得到不失真的采样信号。 naaTnTtTnTtntxtx/)(π]/)(πsin[)()( 这是由时域离散信号理想恢复模拟信号的插值公式。 1.2 解线性卷积的方法 解线性卷积是数字信号处理中的重要运算。 解线性卷积有三种方法, 即图解法(列表法)、 解析法和在计算机上用 MATLAB 语言求解。 它们各有特点。 图解法(列表法)适合于简单情况, 短序列的线性卷积, 因此考试中常用, 不容易得到封闭解。 解析法适合于用公式表示序列的线性卷积, 得到的是封闭解, 考试中会出现简单情况的解析法求解。 解析法求解过程中, 关键问题是确定求和限, 求和限可以借助于画图确定。 第三种方法适合于用计算机求解一些复杂的较难的线性卷积, 实验中常用。 解线性卷积也可用 Z 变换法, 以及离散傅里叶变换求解, 这是后面几章的内容。 下面通过例题说明。 设x(n)=R4(n), h(n)=R4(n), 求 y(n)=x(n)*h(n)。 该题是两个短序列的线性卷积, 可以用图解法(列表法)或者解析法求解。 表 1.2.1给出了图解法(列表法), 用公式可表示为 y(n)={…, 0, 0, 1, 2, 3, 4, 3, 2, 1, 0, 0, …} 下面用解析法求解, 写出卷积公式为 mmmnRmRmnhmxny)()()()()(44 在该例题中, R4(m)的非零区间为0≤m≤3, R4(n-m)的非零区间为0≤n-m≤3, 或写成 n-3≤m≤n,这样 y(n)的非零区间要求 m 同时满足下面两个不等式: 0≤m≤3 m-3≤m≤n 上面公式表明 m 的取值和 n 的取值有关, 需要将 n 作分段的假设。 按照上式, 当n 变化时, m 应该按下式取值:max{0, n-3}≤m≤min{3, n} 当 0≤n≤3 时,下限应该是 0,上限应该是 n; 当 4≤n≤6 时,下限应该是 n-3,...