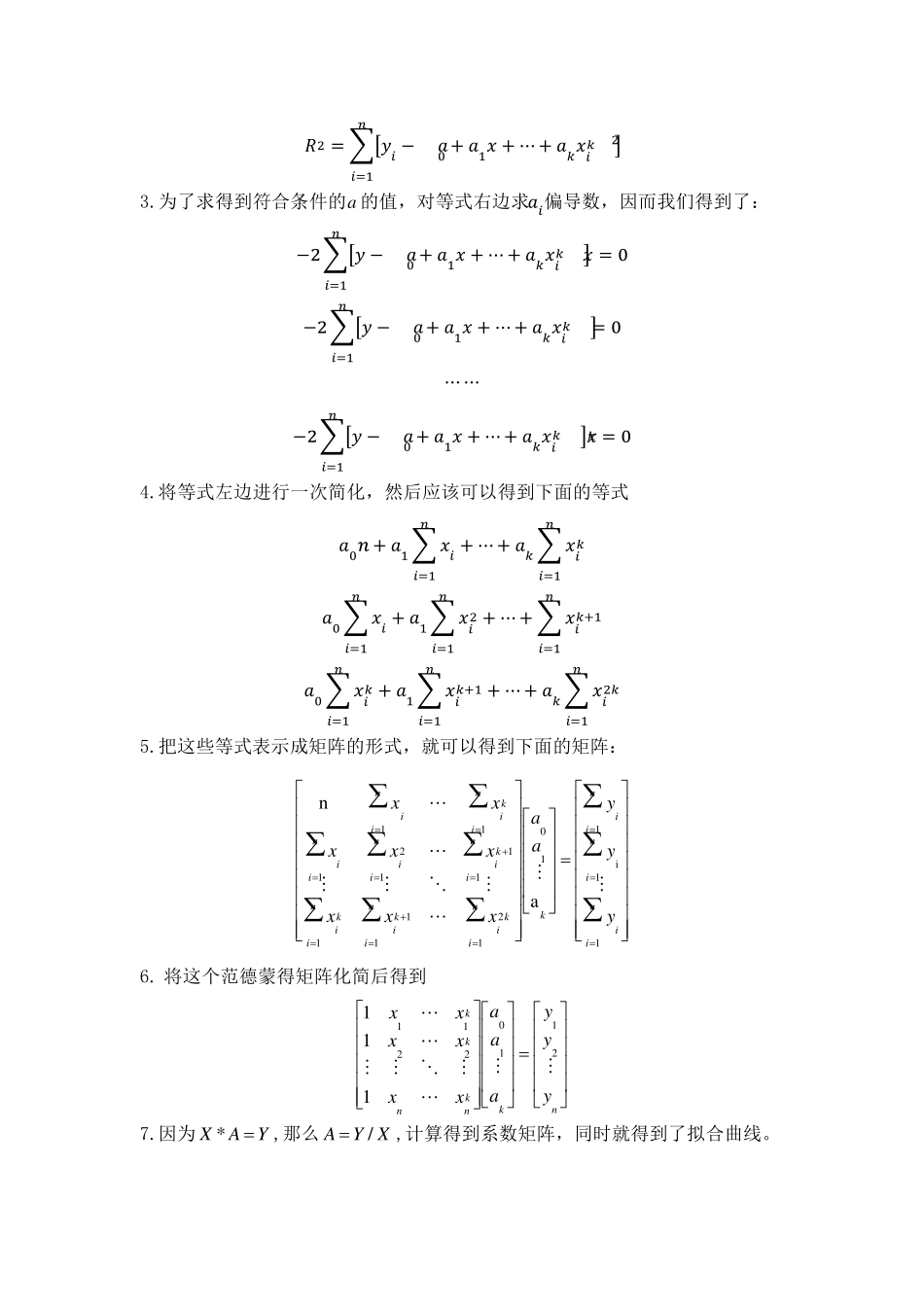
数值分析 课程设计报告 学生姓名 学生学号 所在班级 指导教师 成绩评定 一、课程设计名称 函数逼近与曲线拟合 二、课程设计目的及要求 实验目的: ⑴学会用最小二乘法求拟合数据的多项式,并应用算法于实际问题。 ⑵学会基本的矩阵运算,注意点乘和叉乘的区别。 实验要求: ⑴编写程序用最小二乘法求拟合数据的多项式,并求平方误差,做出离散函数(ᵆᵅ, ᵆᵅ)和拟合函数的图形; ⑵用 MATLAB 的内部函数polyfit 求解上面最小二乘法曲线拟合多项式的系数及平方误差,并用 MATLAB 的内部函数plot 作出其图形,并与(1)结果进行比较。 三、课程设计中的算法描述 用最小二乘法多项式曲线拟合,根据给定的数据点,并不要求这条曲线精确的经过这些点,而是拟合曲线无限逼近离散点所形成的数据曲线。 思 路 分 析 :从 整 体 上 考 虑 近似 函数)(xp同 所 给 数据 点)(ii yx ,误 差iiiyxpr)(的大小,常用的方法有三种:一是误差iiiyxpr)(绝对值的最大值imir0max ,即误差向量的无穷范数;二是误差绝对值的和miir0,即误差向量的1范数;三是误差平方和miir02 的算术平方根,即类似于误差向量的2 范数。前两种方法简单、自然,但不便于微分运算,后一种方法相当于考虑 2 范数的平方,此次采用第三种误差分析方案。 算法的具体推导过程: 1.设拟合多项式为: y = ᵄ0 + ᵄ1ᵆ + ᵄ2ᵆ1 + ⋯ + ᵄᵅᵆᵅ 2.给点到这条曲线的距离之和,即偏差平方和: ᵄ2 = ∑[ᵆᵅ − (ᵄ0 + ᵄ1ᵆ + ⋯ + ᵄᵅᵆᵅᵅ)]2ᵅᵅ=1 3.为了求得到符合条件的a 的值,对等式右边求ᵄᵅ偏导数,因而我们得到了: −2∑[ᵆ − (ᵄ0 + ᵄ1ᵆ + ⋯ + ᵄᵅᵆᵅᵅ)]ᵅᵅ=1ᵆ = 0 −2∑[ᵆ − (ᵄ0 + ᵄ1ᵆ + ⋯ + ᵄᵅᵆᵅᵅ)]ᵅᵅ=1= 0 ⋯ ⋯ −2∑[ᵆ − (ᵄ0 + ᵄ1ᵆ + ⋯ + ᵄᵅᵆᵅᵅ)]ᵆᵅᵅᵅ=1= 0 4.将等式左边进行一次简化,然后应该可以得到下面的等式 ᵄ0ᵅ + ᵄ1 ∑ ᵆᵅ + ⋯ + ᵄᵅ ∑ ᵆᵅᵅᵅᵅ=1ᵅᵅ=1 ᵄ0 ∑ ᵆᵅ + ᵄ1 ∑ ᵆᵅ2 + ⋯ + ∑ ᵆᵅᵅ+1ᵅᵅ=1ᵅᵅ=1ᵅᵅ=1 ᵄ0 ∑ ᵆᵅᵅ + ᵄ1 ∑ ᵆᵅᵅ+1 + ⋯ + ᵄᵅ ∑ ᵆᵅ2ᵅᵅᵅ=1ᵅᵅ=1ᵅᵅ=1 5.把这些等式表示成矩阵的形式,就可以得到下面的矩阵: ...