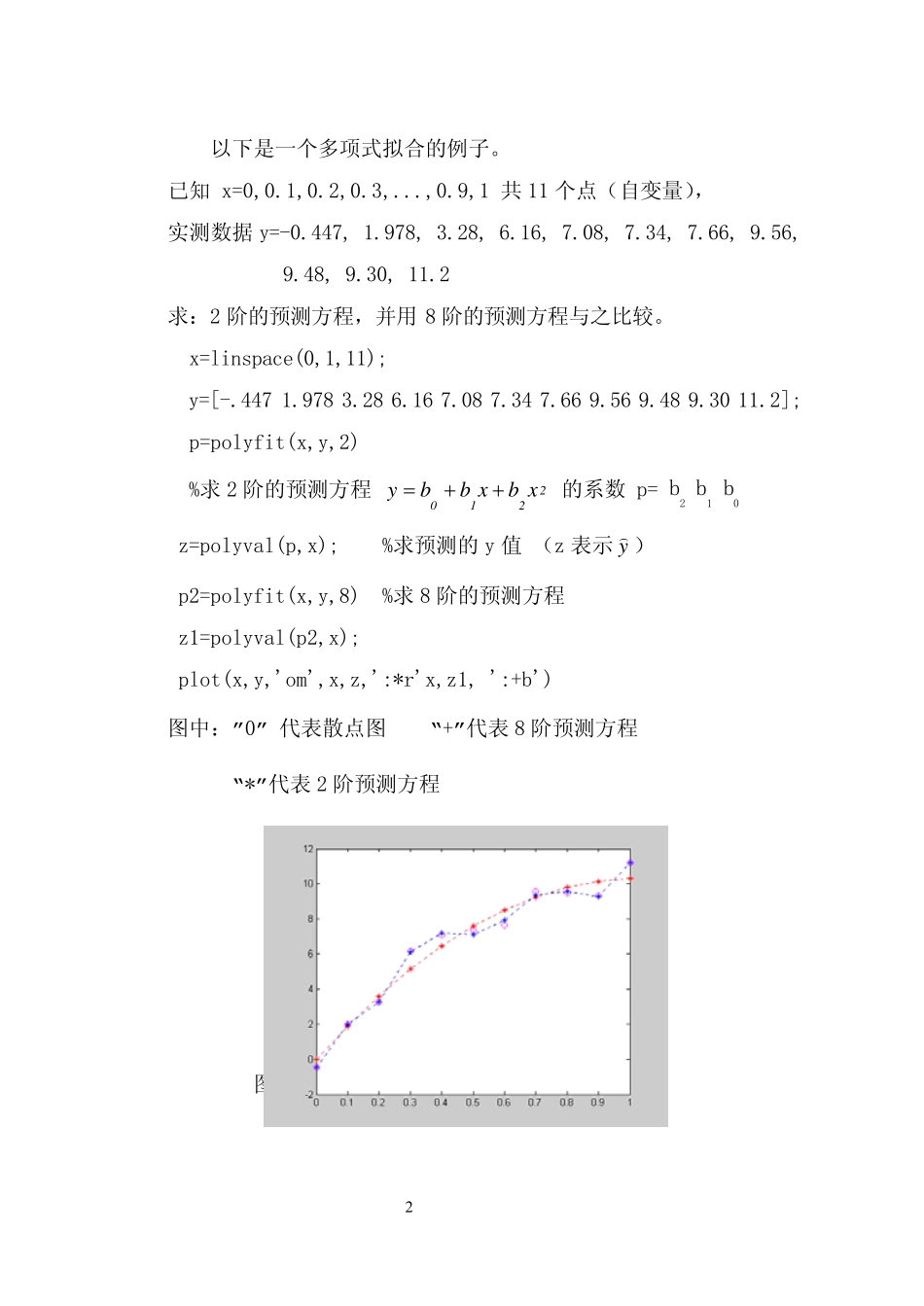
1实验五 最小二乘法及数据拟合建模的回归分析 一、实验目的: 1.掌握用最小二乘建立回归数学模型。 2.学习通过几个数据拟合的回归分析来判断曲线(直线)拟合的精度,通过回归分析来判断模型建立是否正确。 3.应用建立的模型进行预测。 二、基本原理和方法 1.建立回归数学模型 在进行建模和仿真分析时,人们经常面临用已知系统实测数据应用数学模型描述对应系统,即对数据进行拟合。拟合的目的是寻找给定的曲线(直线),它在某种准则下最佳地拟合数据。最佳拟合要在什么准则下的最佳?以及用什么样的曲线模型去拟合。 常用的拟合方法之一是多项式的最小二乘拟合,其准则是最小误差平方和准则,所用的拟合曲线为多项式。 本实验在 Matlab 平台上,以多项式最小二乘拟合为例,掌握回归模型的建立(包括参数估计和模型建立)和用模型进行预测的方法,并学习回归分析的基本方法。 2.在 MATLAB 里,用于求解最小二乘多项式拟合问题的函数如下: polyfit 最小二乘多项式拟合 p=polyfit(x,y,n) 对输入数据y的n阶最小二乘拟合多项式p(x)的系数 Y=polyval(p,x) 求多项式的函数值 Y )1n(px)n(px)2(px)1(pY1nn+++++=−L 2以下是一个多项式拟合的例子。 已知 x=0,0.1,0.2,0.3,...,0.9,1 共 11 个点(自变量), 实测数据 y=-0.447, 1.978, 3.28, 6.16, 7.08, 7.34, 7.66, 9.56, 9.48, 9.30, 11.2 求:2 阶的预测方程,并用 8 阶的预测方程与之比较。 x=linspace(0,1,11); y=[-.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2]; p=polyfit(x,y,2) %求 2 阶的预测方程 2210xbxbby++= 的系数 p= b2 b1 b0 z=polyval(p,x); %求预测的y 值 (z 表示 y) ) p2=polyfit(x,y,8) %求 8 阶的预测方程 z1=polyval(p2,x); plot(x,y,'om',x,z,':*r'x,z1, ':+b') 图中:”0” 代表散点图 “+”代表 8 阶预测方程 “*”代表 2 阶预测方程 图 1 散点图与 2 阶预测方程 33.回归模型的检验 回归模型的检验是判断数据拟合的好坏即模型建立的正确与否,为建立模型和应用模型提供支持。 在MATLAB 平台,用于回归检验的语句如下: [b,bint,r,rint,stats]=regress(y,X,α) 其中,01 122mmyxxxe= β +β+β++β+L )m,2,1,0i(iL=β为回归系数 e 随机误差(均值为0,方差2σ ) b:回归系数的估计值 ˆb = β bint:回归系数的置信区间 r:残差 yy...