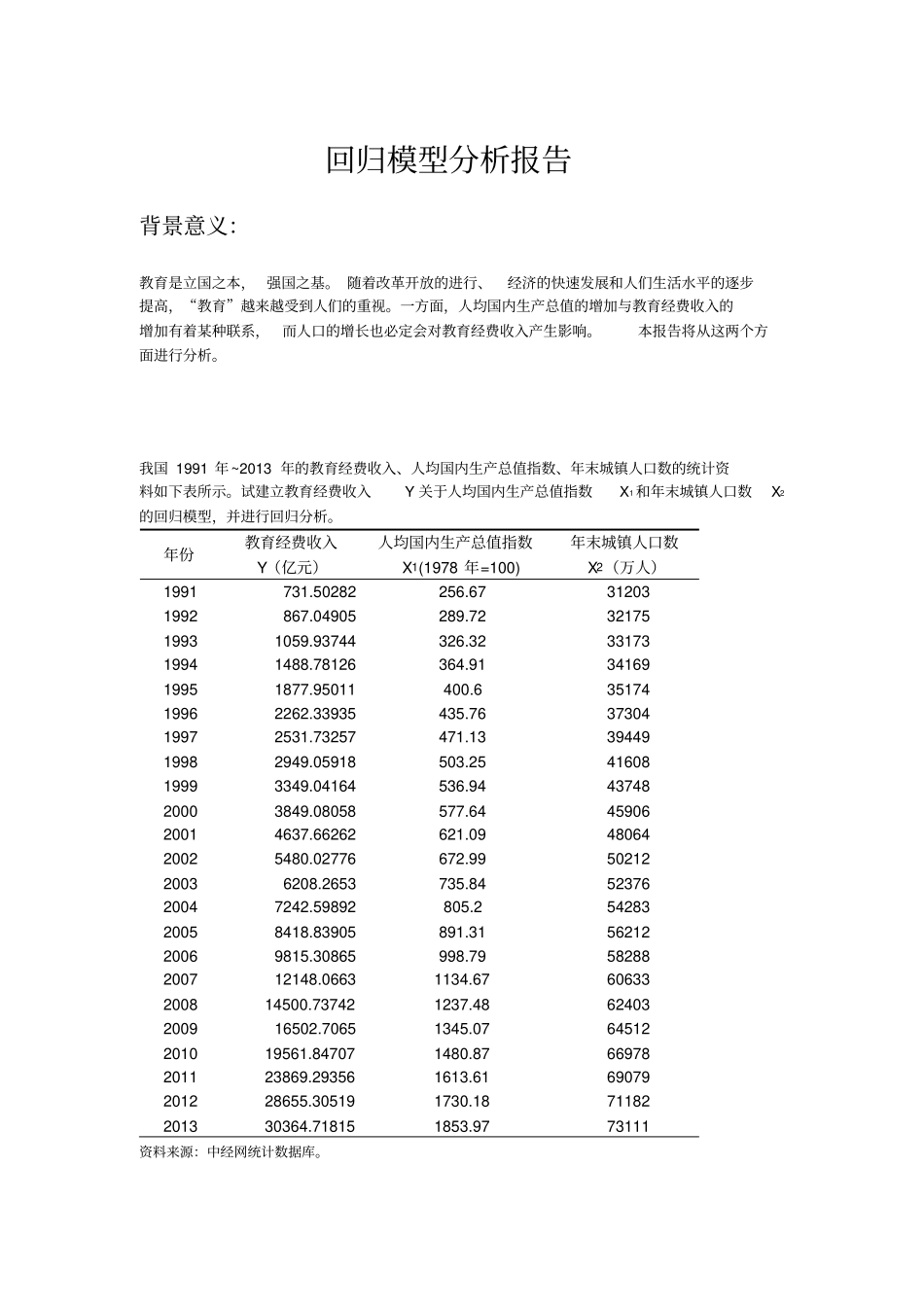
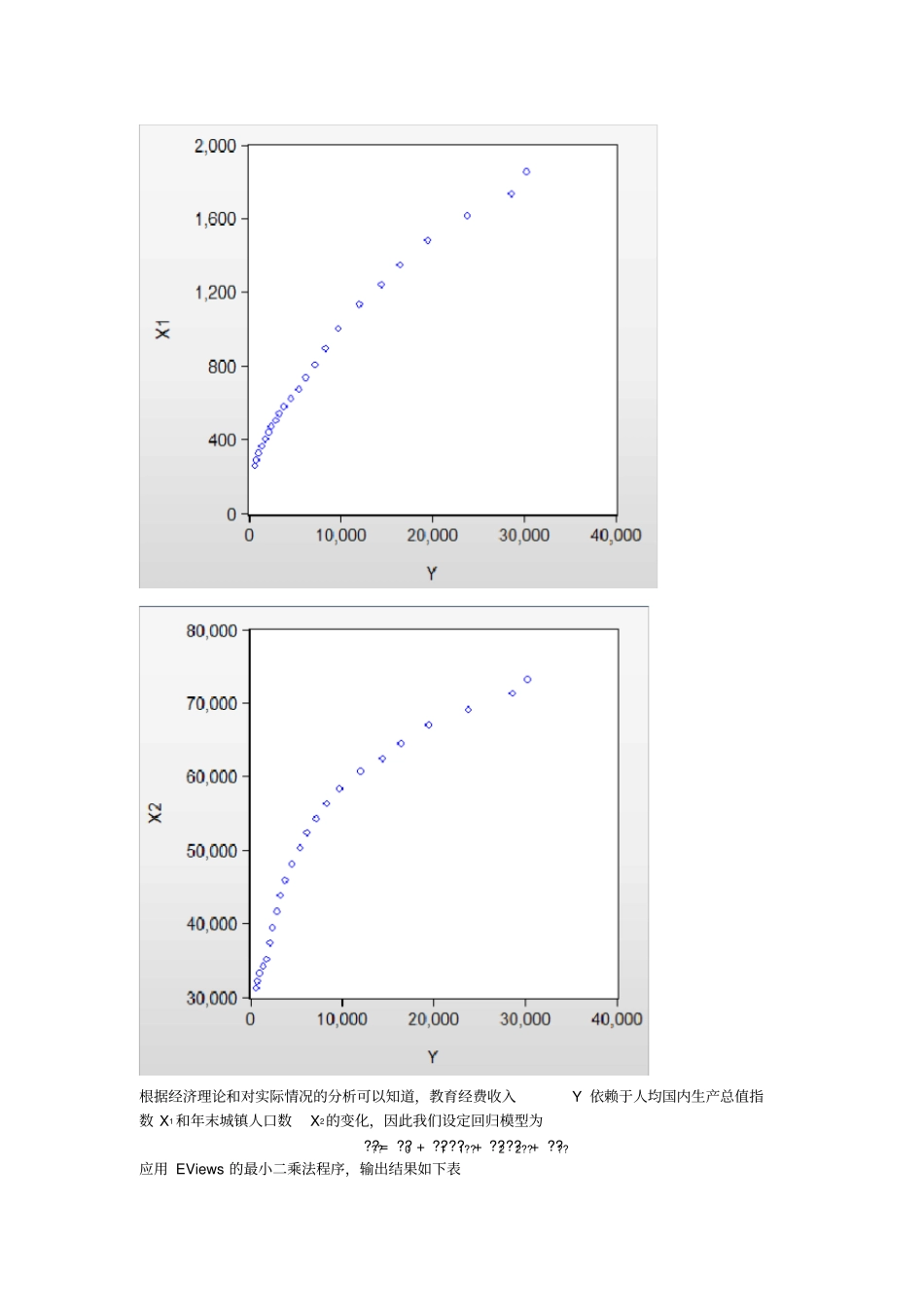
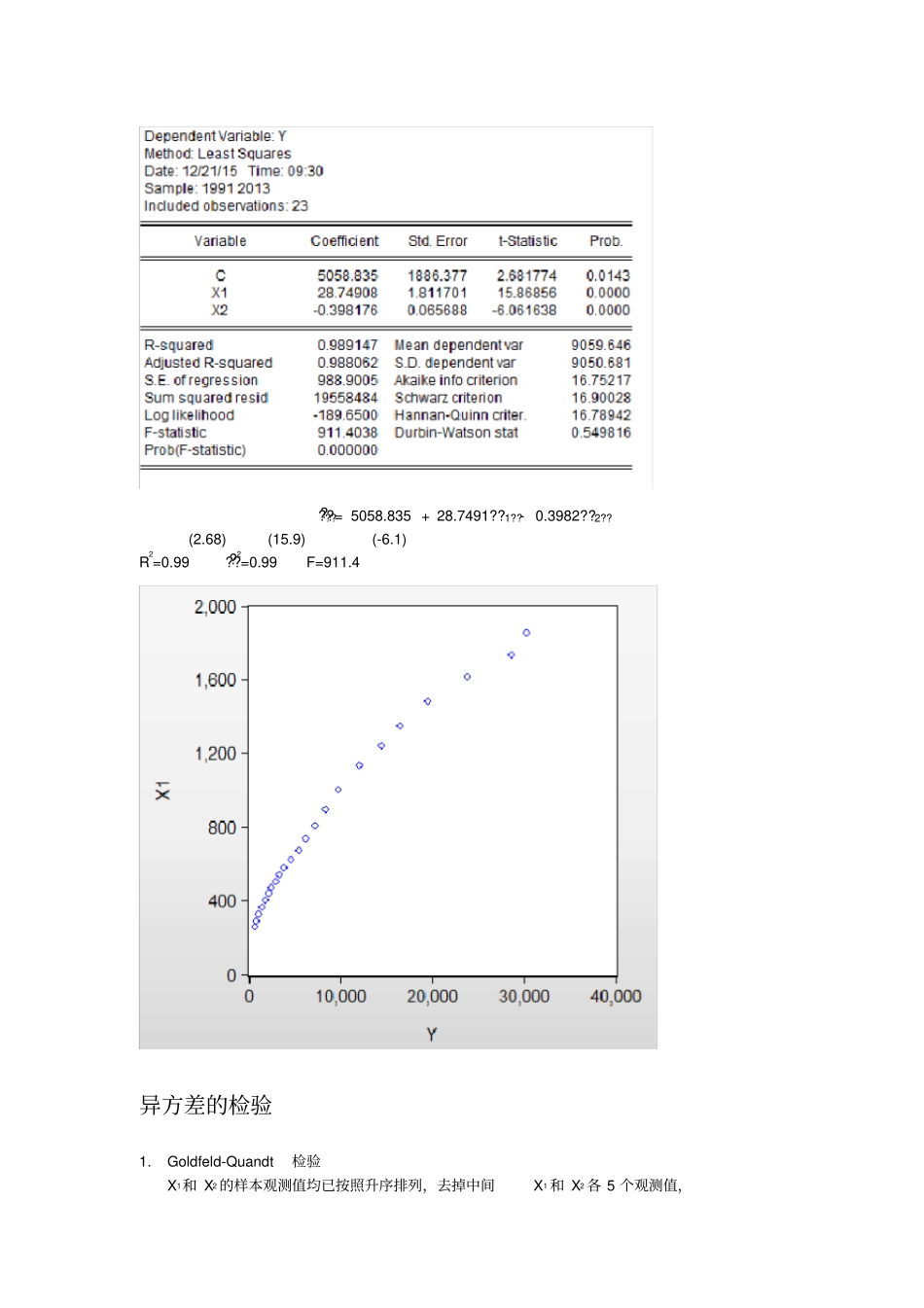
回归模型分析报告背景意义:教育是立国之本, 强国之基。 随着改革开放的进行、经济的快速发展和人们生活水平的逐步提高,“教育”越来越受到人们的重视。一方面,人均国内生产总值的增加与教育经费收入的增加有着某种联系,而人口的增长也必定会对教育经费收入产生影响。本报告将从这两个方面进行分析。我国 1991 年~2013 年的教育经费收入、人均国内生产总值指数、年末城镇人口数的统计资料如下表所示。试建立教育经费收入Y 关于人均国内生产总值指数X1 和年末城镇人口数X2的回归模型,并进行回归分析。年份教育经费收入Y(亿元)人均国内生产总值指数X1(1978 年=100) 年末城镇人口数X2(万人)1991 731.50282 256.67 31203 1992 867.04905 289.72 32175 1993 1059.93744 326.32 33173 1994 1488.78126 364.91 34169 1995 1877.95011 400.6 35174 1996 2262.33935 435.76 37304 1997 2531.73257 471.13 39449 1998 2949.05918 503.25 41608 1999 3349.04164 536.94 43748 2000 3849.08058 577.64 45906 2001 4637.66262 621.09 48064 2002 5480.02776 672.99 50212 2003 6208.2653 735.84 52376 2004 7242.59892 805.2 54283 2005 8418.83905 891.31 56212 2006 9815.30865 998.79 58288 2007 12148.0663 1134.67 60633 2008 14500.73742 1237.48 62403 2009 16502.7065 1345.07 64512 2010 19561.84707 1480.87 66978 2011 23869.29356 1613.61 69079 2012 28655.30519 1730.18 71182 2013 30364.71815 1853.97 73111 资料来源:中经网统计数据库。根据经济理论和对实际情况的分析可以知道,教育经费收入Y 依赖于人均国内生产总值指数 X1 和年末城镇人口数X2的变化,因此我们设定回归模型为????= ??0 + ??1 ??1??+ ??2??2??+ ????应用 EViews 的最小二乘法程序,输出结果如下表?????= 5058.835 + 28.7491??1??- 0.3982??2??(2.68) (15.9) (-6.1) R2=0.99 ???2=0.99 F=911.4 异方差的检验1.Goldfeld-Quandt检验X1和 X2 的样本观测值均已按照升序排列,去掉中间X1 和 X2 各 5 个观测值,用第一个子样本回归:?????= -3510.668+ 5.9096??1??+ 0.0839??2??SSE1=45633.64用第二个子样本回归:?????= 178636.6 + 107.5861??1??- 4.7488??2??SSE2=6602898H0=u t 具有同方差,H1=u t 具有递增型异方差构...