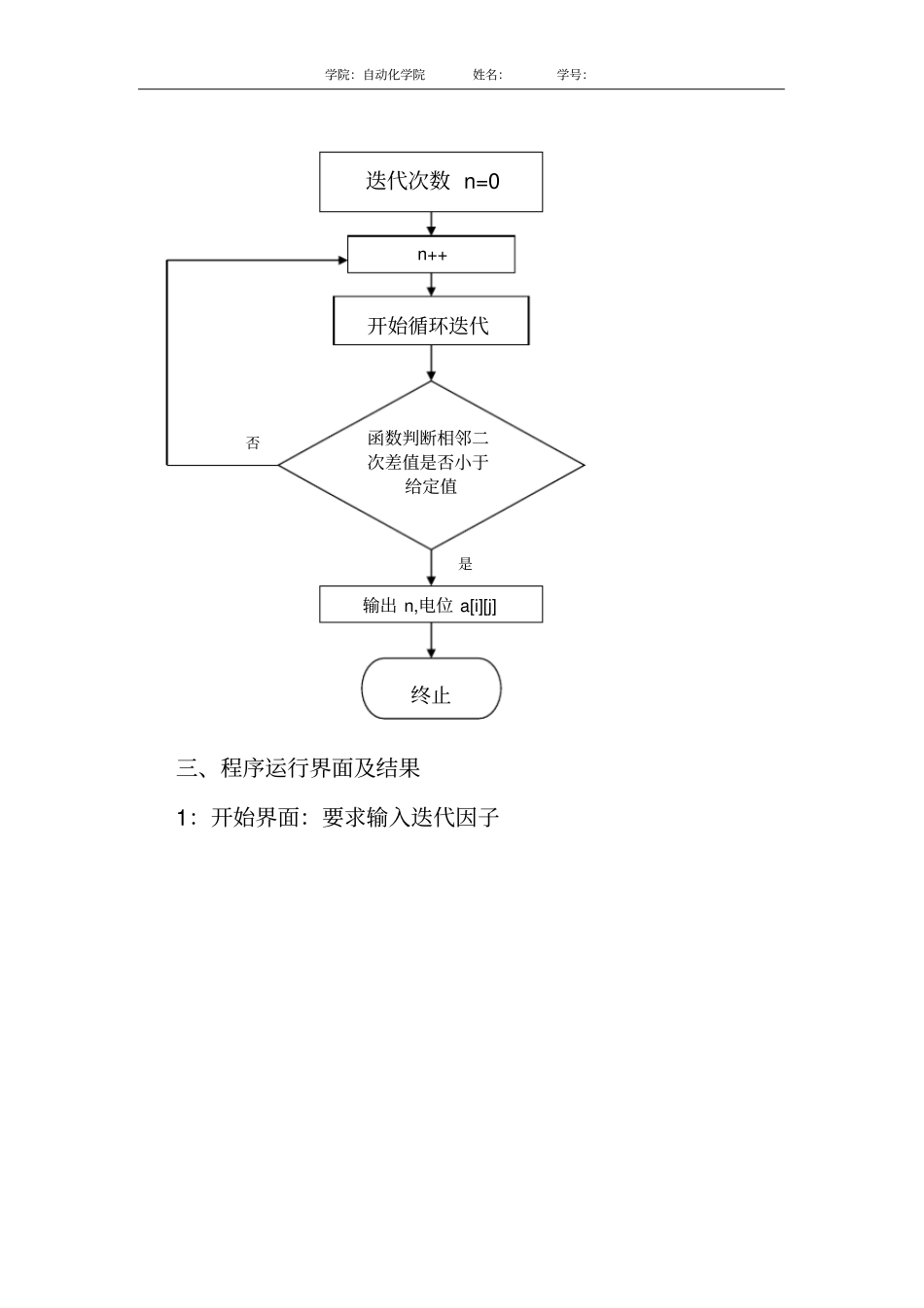
学院:自动化学院姓名:学号:实验一 用超松弛迭代法求解接地金属槽内电位分布学院:自动化学院姓名:学号:一、实验内容:试用超松弛迭代法求解接地金属槽内电位的分布。已知:cma4,mmah104/给定边值如图所示。给定初值:0)0(, ji误差范围:510计算迭代次数,ji , 分布。二.实验设计原理:有限差分法有限差分法( Finite Differential Method)是基于差分原理的一种数值计算法。其基本思想:将场域离散为许多小网格,应用差分原理,将求解连续函数?的泊松方程的问题换为求解网格节点上?的差分方程组的问题。编程时已经考虑到题目要求,所以直接将边值编入到程序中,这样可以省略输入, 从而直接输入迭代因子进行求解,可以减少编程的难度。这次编程和以前不同的是将数组和正0V100 00学院:自动化学院姓名:学号:交函数图像结合起来,所以在考虑输入和输出的时候会有一些难度,因为数组是上面是小的而图像上面越在上,代表坐标就越大。所以在输入和输出的时候要谨慎对待。迭代时所用公式是和书上一样,为a[i][j]=b[i][j]+w/4*(b[i+1][j]+b[i][j+1]+a[i][j-1]+a[i-1][j]-4*b[i][j]); 其中 a代表 k+1,而 b代表 k。以上分析了迭代程序的实现,但是迭代循环如何终止并未说明。题目中的误差范围ε=0.00001 ,即当两次迭代结果相差不超过ε 时停止,这里只得是九点都满足不超过ε ,而并不是其中某一点达到即可。这样可以保证不是陷入死循环,从而输出结果。这样可以画出流程图如下所示:启动输出开始菜单(边值都已经给定)输入迭代因子 w 学院:自动化学院姓名:学号:否是三、程序运行界面及结果1:开始界面:要求输入迭代因子迭代次数 n=0 n++ 开始循环迭代函数判断相邻二次差值是否小于给定值输出 n,电位 a[i][j] 终止学院:自动化学院姓名:学号:2:输入迭代因子进行计算:如输入1.18 可以求出结果,得知要进行12次迭代。四.源程序代码#include #include int n=0,m=0,k=0,i=0,j=0; 学院:自动化学院姓名:学号:float w; float a[5][5],b[5][5]; void cjc() //定义函数名{ while(1) { for( j=1;j<4;j++) for( i=1;i<4;i++) { a[i][j]=b[i][j]+w/4*(b[i+1][j]+b[i][j+1]+a[i][j-1]+a[i-1][j]-4*b[i][j]); } //函数运算迭代公式n++; for(i=1;i<4;i++) for(j=1;j<4;j++) { if(fabs(a[i][j]-b[i][j])<0.00001) //保证误差,从而能够确保输出,不必陷入死循环k++; } if...