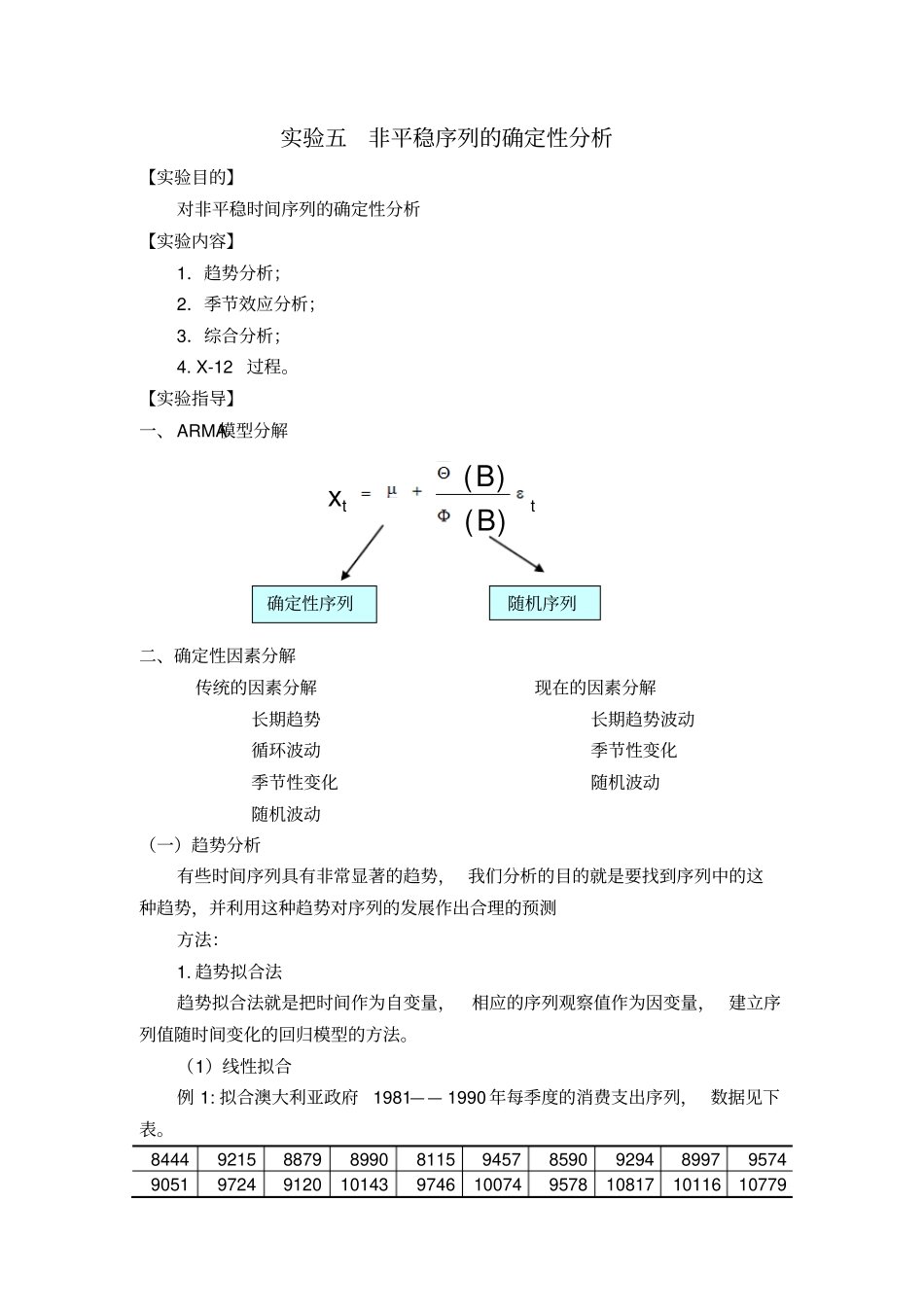
实验五非平稳序列的确定性分析【实验目的】对非平稳时间序列的确定性分析【实验内容】1.趋势分析;2.季节效应分析;3.综合分析;4. X-12 过程。【实验指导】一、 ARMA模型分解二、确定性因素分解传统的因素分解长期趋势循环波动季节性变化随机波动现在的因素分解长期趋势波动季节性变化随机波动(一)趋势分析有些时间序列具有非常显著的趋势, 我们分析的目的就是要找到序列中的这种趋势,并利用这种趋势对序列的发展作出合理的预测方法:1. 趋势拟合法趋势拟合法就是把时间作为自变量,相应的序列观察值作为因变量, 建立序列值随时间变化的回归模型的方法。(1)线性拟合例 1: 拟合澳大利亚政府1981—— 1990 年每季度的消费支出序列, 数据见下表。8444 9215 8879 8990 8115 9457 8590 9294 8997 9574 9051 9724 9120 10143 9746 10074 9578 10817 10116 10779 ttBBx)()(确定性序列随机序列9901 11266 10686 10961 10121 11333 10677 11325 10698 11624 11052 11393 10609 12077 11376 11777 11225 12231 11884 12109 800090001000011000120001300081828384858687888990GOV_CONS长期趋势呈现出非常的线性递增趋势,于是考虑使用线性模型2,1,2,...40()0,()ttttxabtI tE IVar I拟合该序列的发展。使用最小二乘法得到未知参数的估计值为:??8498.69,89.12ab. 对拟合模型进行检验, 检验结果显示方程显著成立,且参数非常显著。 拟合效果图如下:800090001000011000120001300081828384858687888990FGOV_CONSGOV_CONS(2)非线性拟合使用场合: 长期趋势呈现出非线形特征参数估计指导思想: 能转换成线性模型的都转换成线性模型,用线性最小二乘法进行参数估计;实在不能转换成线性的,就用迭代法进行参数估计例 2: 对上海证券交易所 1991年 1 月-2001 年 10 月每月末上证指数序列进行模型拟合数据见下表。130.44 133.47 120.19 113.94 114.83 137.56 143.8 178.43 180.92 218.6 259.6 292.75 313.24 364.66 381.24 445.38 1234.71 1191.19 1052.07 823.27 702.32 507.25 724.6 780.39 1198.48 1339.88 925.91 1358.78 935.48 1007.05 881.07 895.68 890.27 814.82 984.93 833.8 770.25 770.98 704.46 592.56 556.26 469.29 333.92 785.33 791.15 654.98 683.59 647.87 562.59 549.26 646.92 579.93 700.51 630.58 6...