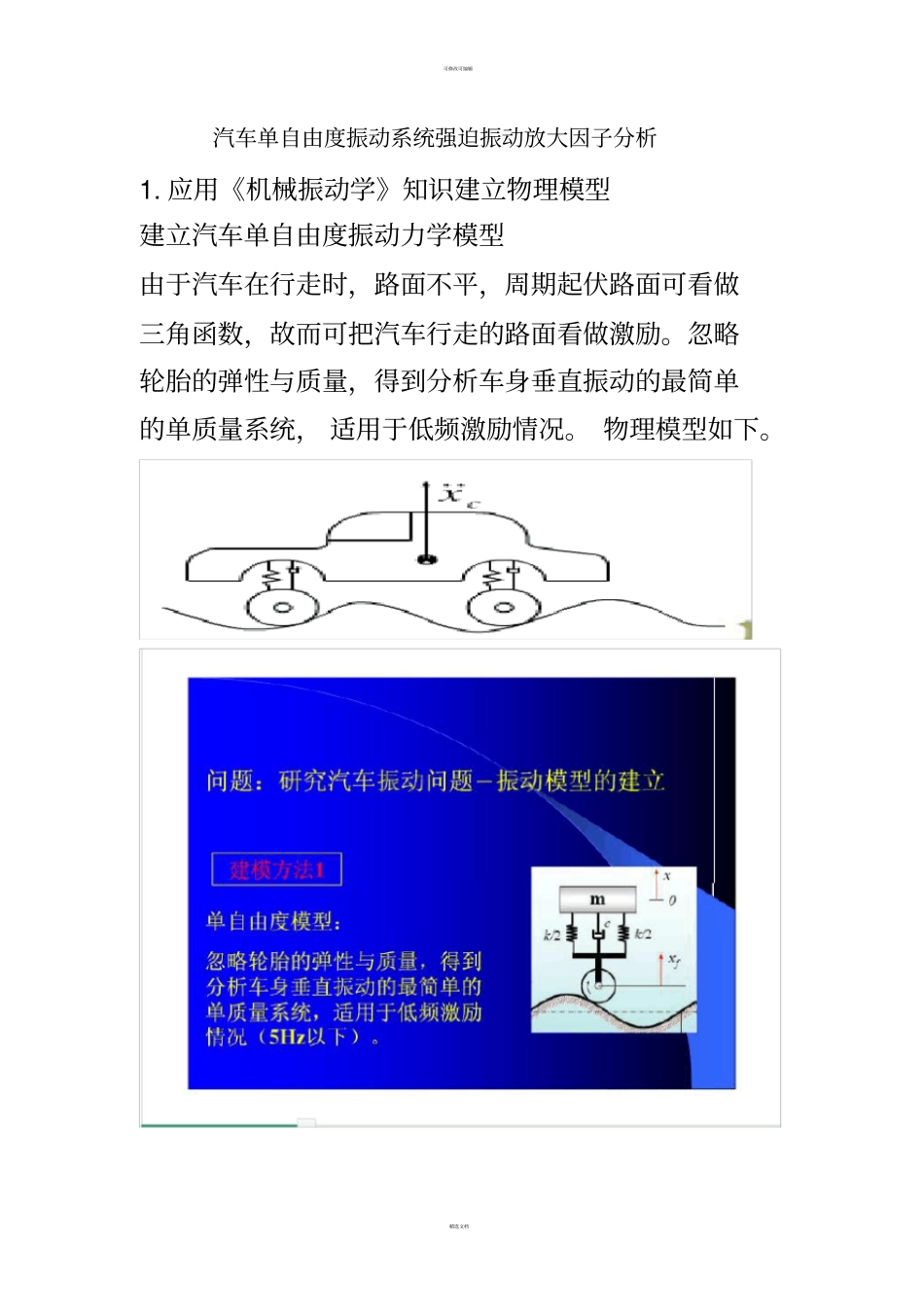
可修改可编辑精选文档汽车单自由度振动系统强迫振动放大因子分析1. 应用《机械振动学》知识建立物理模型建立汽车单自由度振动力学模型由于汽车在行走时,路面不平,周期起伏路面可看做三角函数,故而可把汽车行走的路面看做激励。忽略轮胎的弹性与质量,得到分析车身垂直振动的最简单的单质量系统, 适用于低频激励情况。 物理模型如下。可修改可编辑精选文档其中 xf =y=Y sin(wt) 其中 k 为弹性系数, c 为阻尼系数。2. 根据所建立的力学模型列出微分方程根据牛顿定律,写出数学方程。"''mxk xyc xy"''mxcxkxcyky ⑴由此可见。基础运动使系统受两个作用力,一个是与y(t) 同相位,经弹簧传给质m的力 ky;一个是与速度y’同相位,经阻尼器传给质量m的力 cy’。利用复指数法求解,用sinjwtYeYwt ,并假定方程的解为jwtx txe ,代入方程( 1)得22221212rXYrr可表示为可修改可编辑精选文档22221212rXYrr阻尼比02cccmk c 为阻尼系数,0c 为临界阻尼系数频率比nwrw ,w为激励频率,nw为系统固有频率。3 利用 MATALB编程y1=sqrt((1+(2*0.1*x).^2)/((1-x.^2).^2+(2*0.1*x).^2)); y2=sqrt((1+(2*0.15*x).^2)/((1-x.^2).^2+(2*0.15*x).^2)); y3=sqrt((1+(2*0.25*x).^2)/((1-x.^2).^2+(2*0.25*x).^2)); y4=sqrt((1+(2*0.5*x).^2)/((1-x.^2).^2+(2*0.5*x).^2)); ezplot('y1=sqrt((1+(2*0.1*x).^2)/((1-x.^2).^2+(2*0.1*x).^2))',[0,6]); hold on; ezplot('y2=sqrt((1+(2*0.15*x).^2)/((1-x.^2).^2+(2*0.15*x).^2))',[0,6]) ezplot('y3=sqrt((1+(2*0.25*x).^2)/((1-x.^2).^2+(2*0.25*x).^2))',[0,6]) ezplot('y4=sqrt((1+(2*0.5*x).^2)/((1-x.^2).^2+(2*0.5*x).^2))',[0,6]); 可修改可编辑精选文档title('放大因子 X/Y 与频率比 r 的曲线 ') xlabel('频率比 ') ylabel('放大因子 X/Y') text(x(20),5,'阻尼比 0.1') text(x(20),3,'阻尼比 0.15') text(x(20),2,'阻尼比 0.25') text(x(20),1,'阻尼比 0.5')可修改可编辑精选文档把程序写入 MATALB,用软件开始编程运行程序得如下结果可修改可编辑精选文档再把该图形做完整XY 以 为参数,随 r 变化的曲线表示如下图。现在经过建立物理模型,构建数学模型,再利用MATALB仿真,最终得出了汽车振动系统强迫振动下的频率放大因子图形。分析:当0r时,1M,而与阻尼无关。这意味着,当激励频率接近于零时,振幅与静位移相近。当 r时,0M。也与阻尼大小无关。...