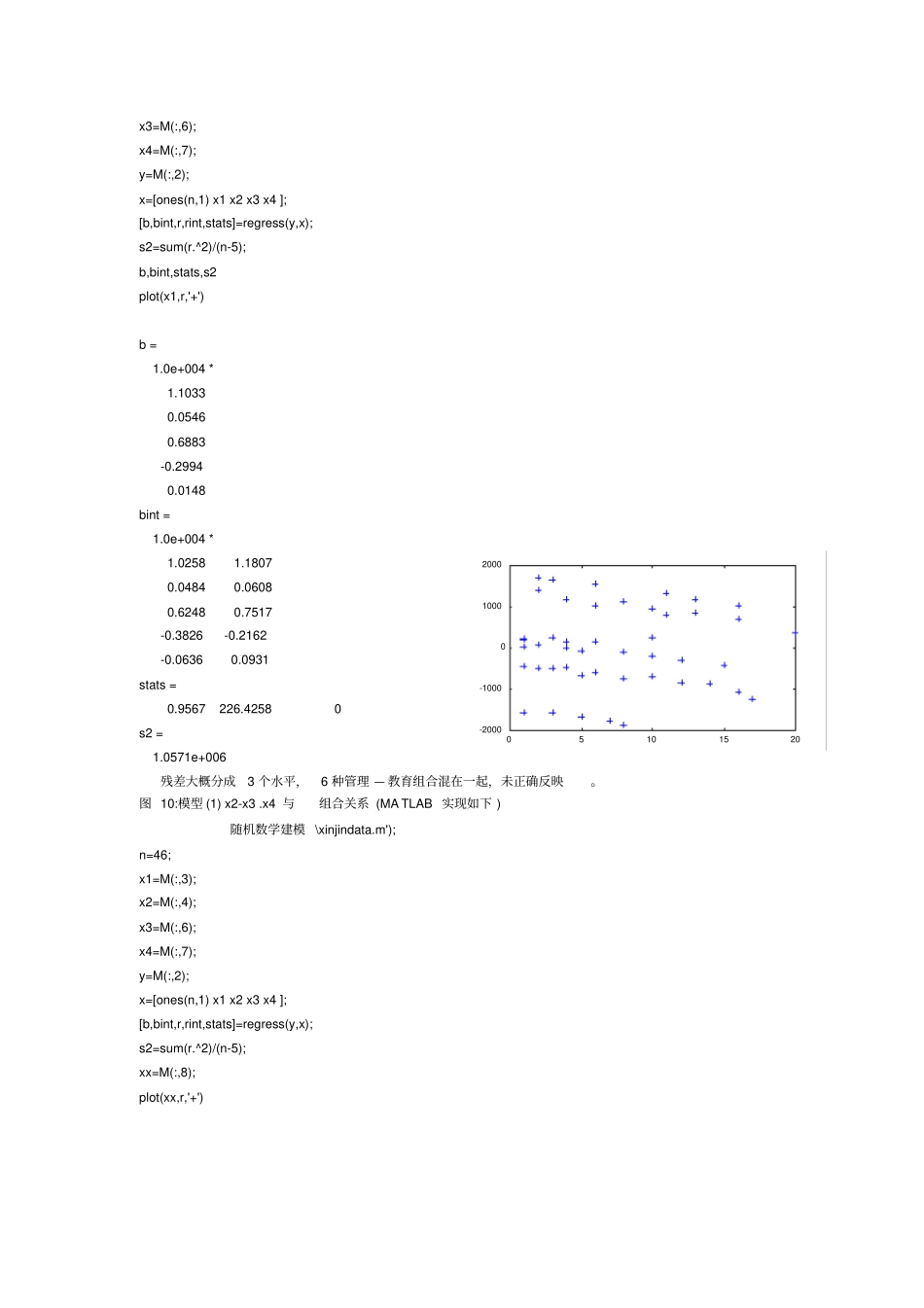
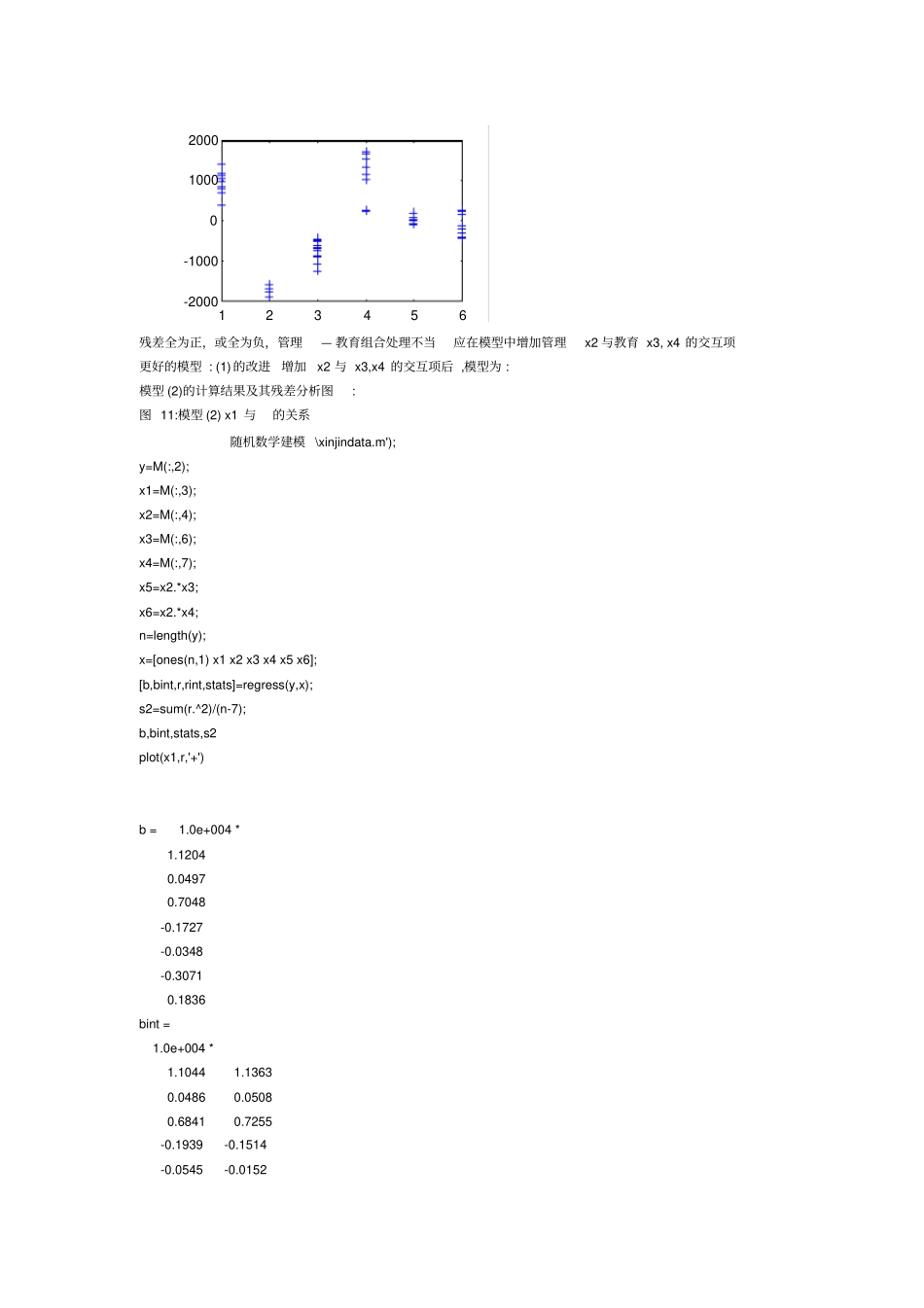
建立模型研究薪金与资历、管理责任、教育程度的关系,分析人事策略的合理性,作为新聘用人员薪金的参考 46 名软件开发人员的档案资料资历 ~ 从事专业工作的年数;管理~ 1=管理人员, 0=非管理人员;教育~ 1=中学, 2=大学, 3=更高程度分析与假设y~ 薪金, x1 ~资历(年)x2 = 1~ 管理人员, x2 = 0~ 非管理人员教育 1=中学 2=大学 3=更高其它中学,0,13x其它大学,0,14x中学:x3=1, x4=0 ;大学:x3=0, x4=1; 更高:x3=0, x4=0 线性回归模型443322110xaxaxaxaaya0, a1, ⋯ , a4 是待估计的回归系数,是随机误差模型求解软件开发人员的薪金(MA TLAB 实现 ) 基本模型:443322110xaxaxaxaay资历增加 1 年薪金增长546 管理人员薪金多6883 中学程度薪金比更高的少2994 大学程度薪金比更高的多148 a4 置信区间包含零点,解释不可靠! 模型 (1)的计算结果及其残差分析图: 图 9:模型 (1)x1 与的关系随机数学建模 \xinjindata.m'); n=46; x1=M(:,3); x2=M(:,4); 参数参数估计值置信区间a011032 [ 10258 11807 ] a1546 [ 484 608 ] a26883 [ 6248 7517 ] a3-2994 [ -3826 -2162 ] a4148 [ -636 931 ] R2=0.957 F=226 p=0.000 x3=M(:,6); x4=M(:,7); y=M(:,2); x=[ones(n,1) x1 x2 x3 x4 ]; [b,bint,r,rint,stats]=regress(y,x); s2=sum(r.^2)/(n-5); b,bint,stats,s2 plot(x1,r,'+') b = 1.0e+004 * 1.1033 0.0546 0.6883 -0.2994 0.0148 bint = 1.0e+004 * 1.0258 1.1807 0.0484 0.0608 0.6248 0.7517 -0.3826 -0.2162 -0.0636 0.0931 stats = 0.9567 226.4258 0 s2 = 1.0571e+006 残差大概分成3 个水平,6 种管理 — 教育组合混在一起,未正确反映。图 10:模型 (1) x2-x3 .x4 与组合关系 (MA TLAB 实现如下 ) 随机数学建模 \xinjindata.m'); n=46; x1=M(:,3); x2=M(:,4); x3=M(:,6); x4=M(:,7); y=M(:,2); x=[ones(n,1) x1 x2 x3 x4 ]; [b,bint,r,rint,stats]=regress(y,x); s2=sum(r.^2)/(n-5); xx=M(:,8); plot(xx,r,'+') 05101520-2000-1000010002000残差全为正,或全为负,管理— 教育组合处理不当应在模型中增加管理x2 与教育 x3, x4 的交互项更好的模型 : (1)的改进增加x2 与 x3,x4 的交互项后 ,模型为 : 模型 (2)的计算结果及其残差分析图: 图 11:模型 (2) x1 ...