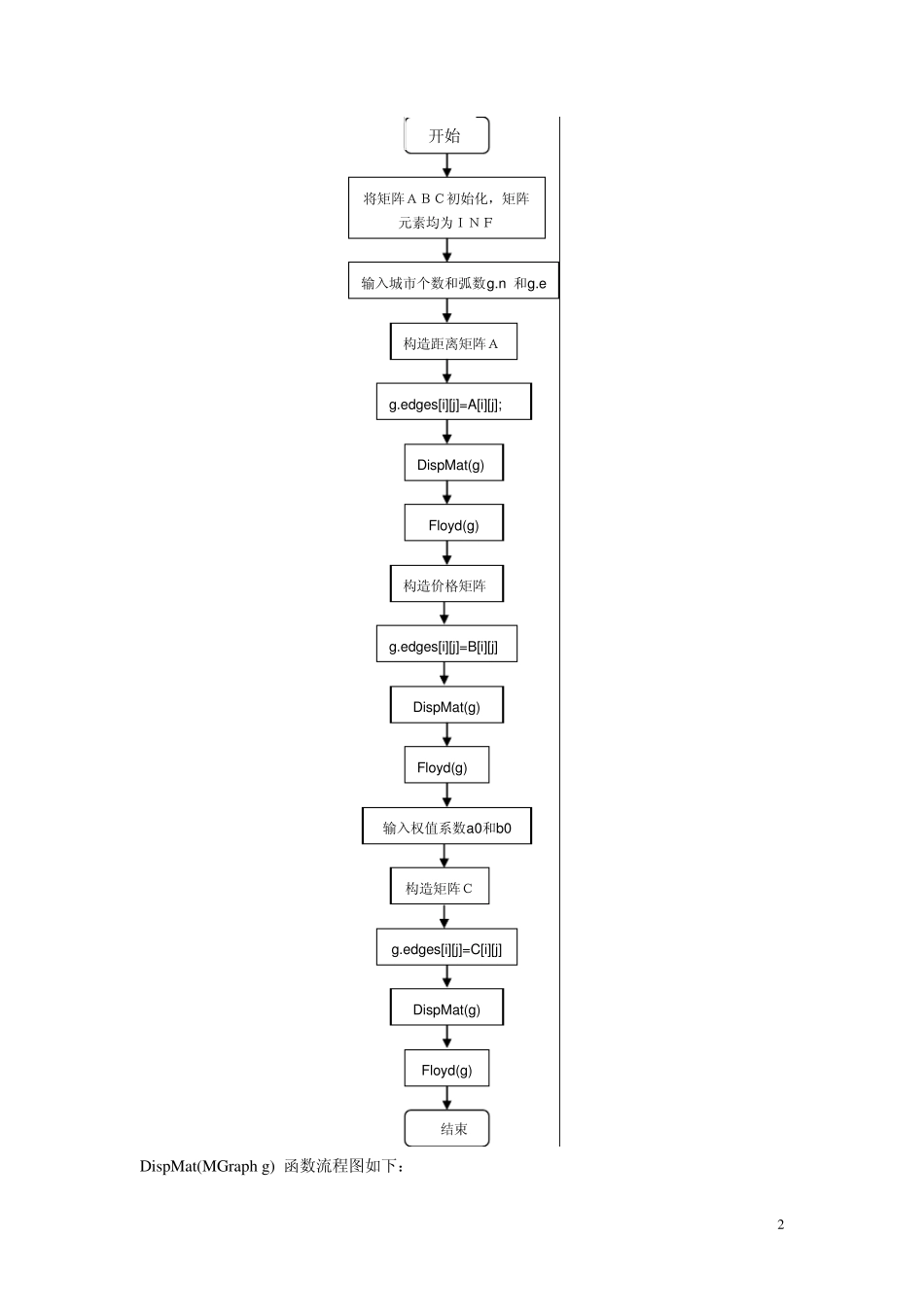
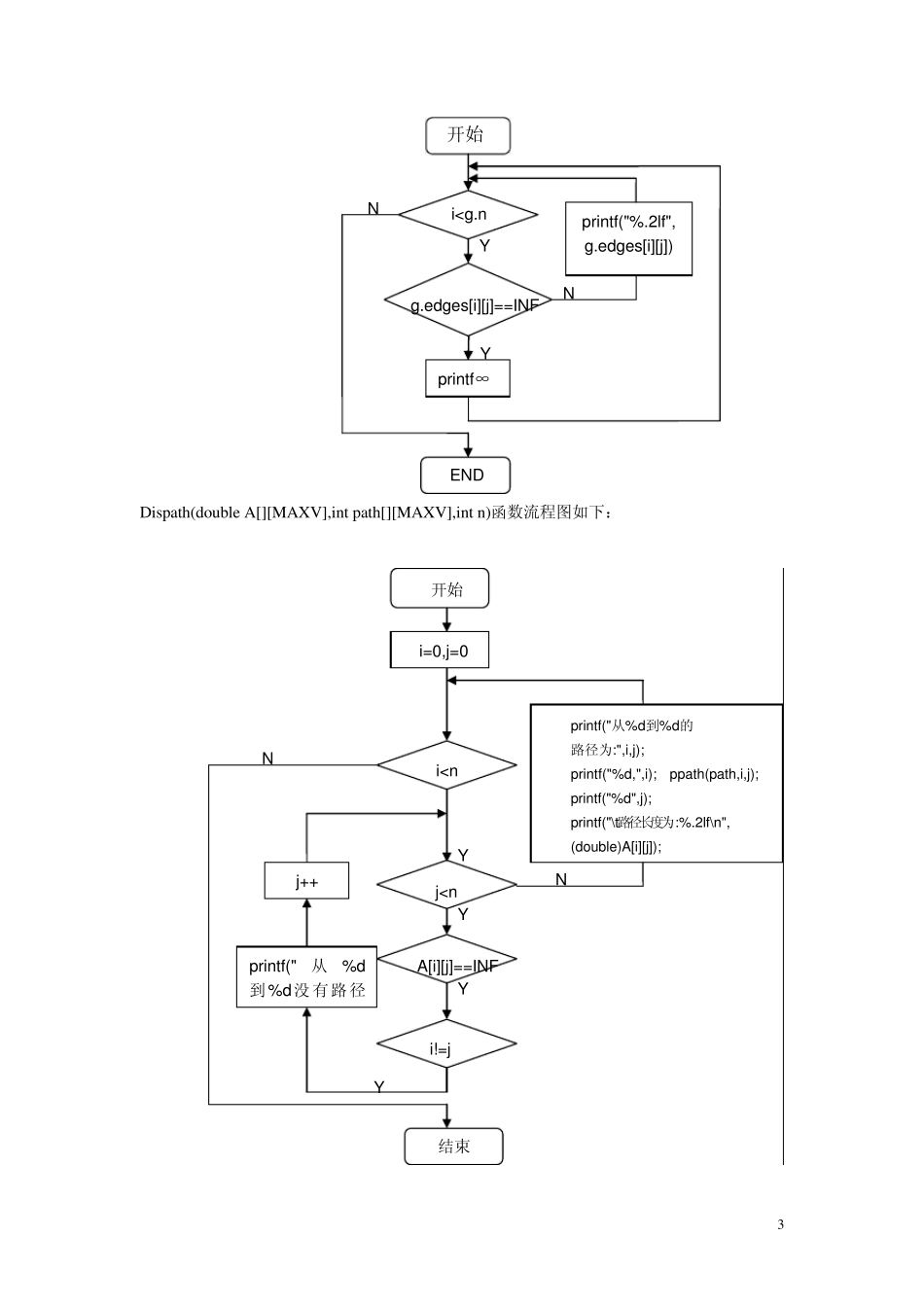
1 实验报告一 一.题目要求 输入N(N<10)个城市,每两个城市之间有对应的距离和费用(可以不能到达),要求实现如下程序: a)给出任意两个城市之间的最短距离,及其到达方式; b)给出任意两个城市之间的最小费用,及其到达方式; c)权衡距离和费用,给出任意两个城市之间的最优路径,及其到达方式; PS:1. 距离矩阵和费用矩阵由同学自己给出; 2. 题 c)的最优路径由自己定义。 二.算法设计: 欲求得每一对顶点之间的最短路径,解决这一问题的办法是采用弗洛伊德算法。 弗洛伊德算法仍从图的带权邻接矩阵出发,其主要思想是:设集合 S 的初始状态为空集合,然后依次向集合 S 中加入顶点 V0,V1,V2,„,Vn-1,每次加入一个顶点,我们用二维数组 D 保存每一对顶点之间的最短路径的长度,其中,D[i][j]存放从顶点Vi 到 Vj 的最短路径的长度。在算法执行中,D[i][j]被定义为:从 Vi 到 Vj 的中间只经过S 中的顶点的所有可能的路径中最短路径的长度(如果从 Vi 到 Vj 中间只经过S 中的顶点当前没有路径相通,那么d[i][j]为一个大值MaxNum)。即d[i][j]中保存的是从 Vi到 Vj 的“当前最短路径”的长度。每次加入一个新的顶点,Vi 和 Vj 之间可能有新的路径产生,将它和已经得到的从 Vi 到 Vj 的最短路径相比较,d[i][j]的值可能需要不断修正,当S=V 时,d[i][j]的值就是从 Vi 到 Vj 的最短路径。 因为初始状态下集合 S 为空集合,所以初始化 D[i][j]=A[i][j](A[i][j]是图的邻接矩阵)的值是从 Vi 直接邻接到 Vj,中间不经过任何顶点的最短路径。当S 中增加了顶点V0,那么D(0)[i][j]的值应该是从 Vi 到 Vj,中间只允许经过v0 的当前最短路径的长度。为了做到这一点,只需对 D(0)[i][j]作如下修改: D(0)[i][j]=min{D[i][j],D[i][0]+D[0][j]} 一般情况下,如果D(k-1)[i][j]是从 Vi 到 Vj,中间只允许经过{ V0,V1,V2,„,Vk-1}的当前最短路径的长度,那么,当S 中加进了 Vk,则应该对 D 进行修改如下: D(k)[i][j]=min{D(k-1)[i][j],D(k-1)[i][k]+D(k-1)[k][j]} 三.概要设计: 1.数据结构 二维数组来表示邻接矩阵,数组中存储元素表示邻接点之间的距离,或费用。 2.抽象数据类型 有向图 3.函数接口 Void main() 主函数 Void Dispmat() 输出邻接矩阵函数 Void Floyed() 计算最短路径函数 Void Dispath() 输出最短路径函数 四.详细设记 Main 函数...