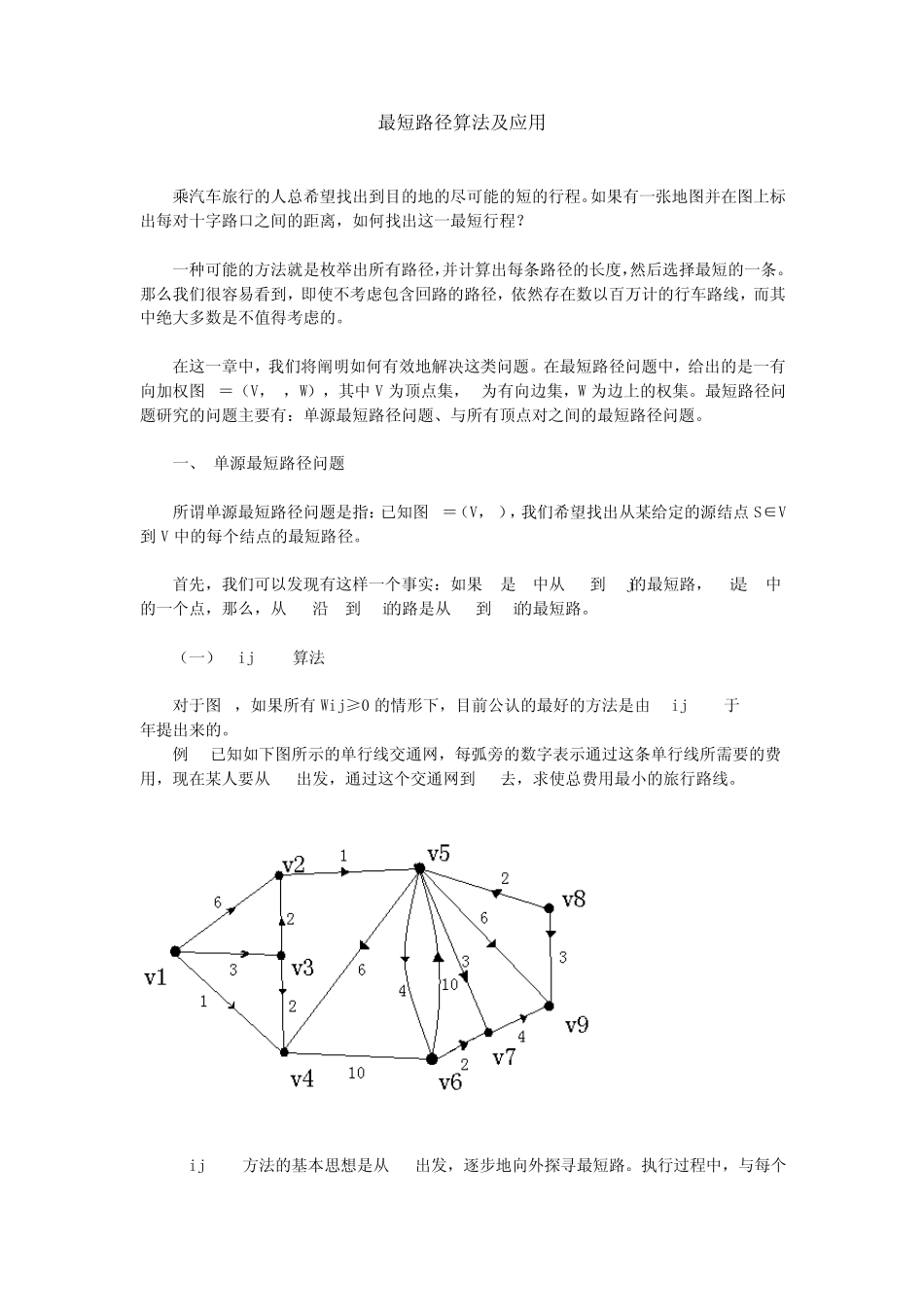
最 短 路 径 算 法 及 应 用 乘 汽 车 旅 行 的 人 总 希 望 找 出 到 目 的 地 的 尽 可 能 的 短 的 行 程 。如 果 有 一 张 地 图 并 在 图 上 标出 每 对 十 字 路 口 之 间 的 距 离 , 如 何 找 出 这 一 最 短 行 程 ? 一 种 可 能 的 方 法 就 是 枚 举 出 所 有 路 径 ,并 计 算 出 每 条 路 径 的 长 度 ,然 后 选 择 最 短 的 一 条 。那 么 我 们 很 容 易 看 到 , 即 使 不 考 虑 包 含 回 路 的 路 径 , 依 然 存 在 数 以 百 万 计 的 行 车 路 线 , 而 其中 绝 大 多 数 是 不 值 得 考 虑 的 。 在 这 一 章 中 , 我 们 将 阐 明 如 何 有 效 地 解 决 这 类 问 题 。 在 最 短 路 径 问 题 中 , 给 出 的 是 一 有向 加 权 图 G= ( V, E, W) , 其 中 V 为 顶 点 集 , E为 有 向 边 集 , W 为 边 上 的 权 集 。 最 短 路 径 问题 研 究 的 问 题 主 要 有 : 单 源 最 短 路 径 问 题 、 与所 有 顶 点 对 之 间 的 最 短 路 径 问 题 。 一 、 单 源 最 短 路 径 问 题 所 谓单 源 最 短 路 径 问 题 是 指: 已知图 G= ( V, E) , 我 们 希 望 找 出 从某给 定的 源 结点 S∈V到 V 中 的 每 个结点 的 最 短 路 径 。 首先, 我 们 可 以 发现有 这 样一 个事实: 如 果 P是 G中 从vs到 vj的 最 短 路 , vi是 P中的 一 个点 , 那 么 , 从vs沿 P到 vi的 路 是 从vs到 vi的 最 短 路 。 ( 一 ) Dijkstra算 法 对 于图 G, 如 果 所 有 Wij≥0 的 情形下, 目 前公认的 最 好的 方 法 是 由 Dijkstra于 1959年提出 来的 。 例 1 已知如 下图 所 示的 单 行 线 交通网, 每 弧旁的 数 字 表示通过这 条 单 行 线 所 需要 的 费用 , 现在 某人 要 从v1出 发, 通过这 个交通网到 v8去, 求使 总 费用 最 小的 旅 行 路 线 。 Dijkstra方 法 的 基本思想是 从vs出 发, 逐步地 向 外探寻最 短 路 。 执行 过程 中 , 与每 个点 对 应...