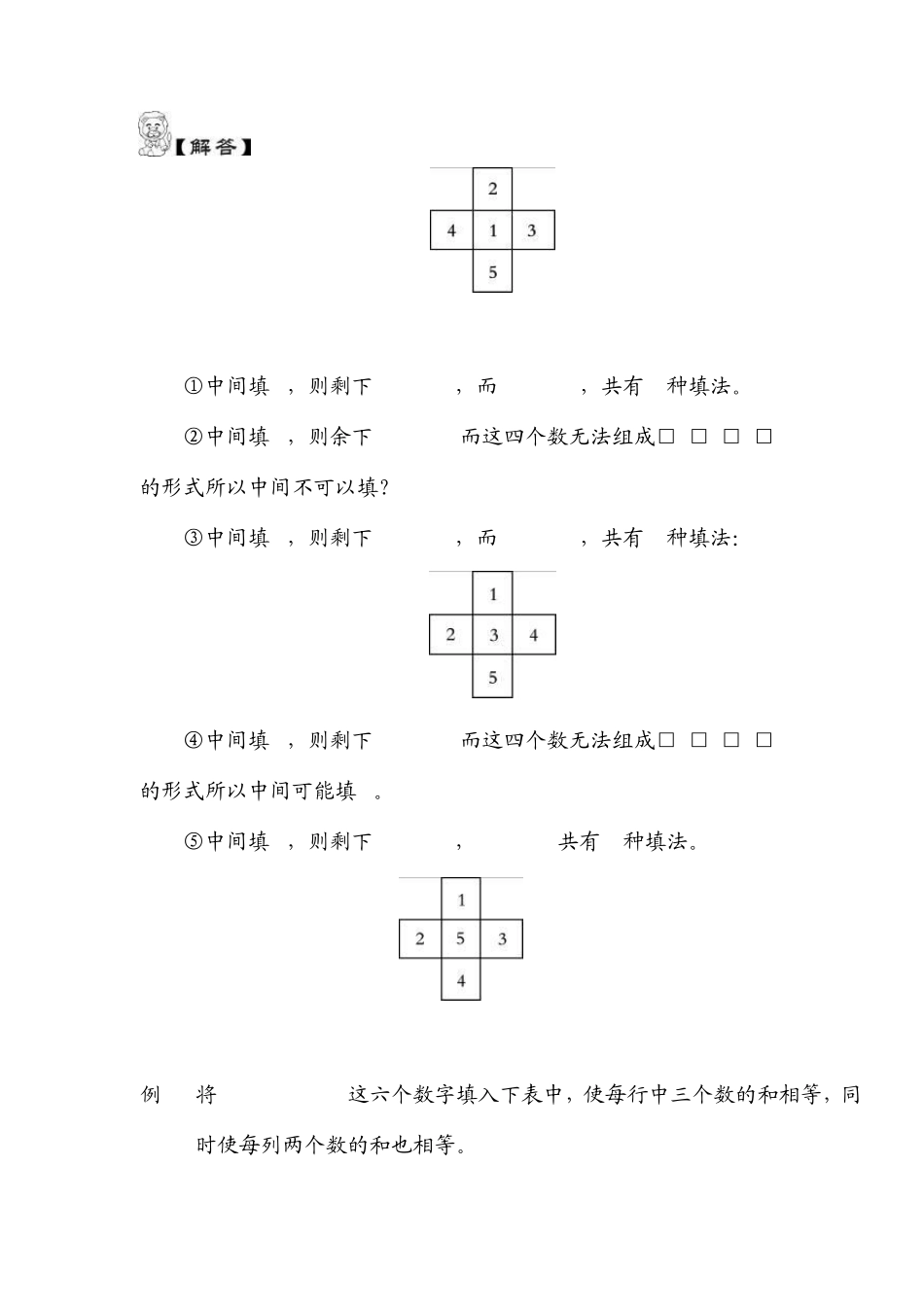
有趣的数阵图 有些数按照一定的要求排列成各种各样的图形,就叫做数阵图, 数阵填数的游戏是非常有趣的,有时也有一定的难度。不过它能促使我们积极地思考问题,分析问题,拓展我们的能力。有的同学说:这样的数阵图填写时只能采取试的方法,没有其他捷径好走。其实这话不对。填写数阵图时,我们应抓住数阵中的关键位置(例如两种线的 交点,长方形和正方形的顶点),再根据题目的要求,进行必要的计算,先填写这些关键位置的数,再填写出其他位置的数。 例1:将1,2,3,4,5这五个数分别填入下图的各正方形中,组成一个“十字数阵图”,使图中横行三个数的和与竖行三个数据的和相等。 根据图形的特点,中间那个数是横行与竖行共用的,要使横行与 竖行三个数的和相等,可以先确定中间的数,再让左右两数的和与上、下两数的和相等。 ①中间填 1,则剩下 2,3,4,5,而 2+5=4+3,共有 8种填法。 ②中间填 2,则余下 1,3,4,5而这四个数无法组成□+□=□+□ 的形式所以中间不可以填? ③中间填 3,则剩下 1,2,4,5,而 1+5=2+4,共有 8种填法: ④中间填 4,则剩下 1,2,3,5而这四个数无法组成□+□=□+□ 的形式所以中间可能填 4。 ⑤中间填 5,则剩下 1,2,3,4,1+4=2+3共有 8种填法。 例1 将 1,2,3,5,6,7这六个数字填入下表中,使每行中三个数的和相等,同时使每列两个数的和也相等。 因为表中有2行、3行,这样六个数可分成(7,3,2)和(6,5,1) 每列两个数的和为24÷3=8,同样这六个数也可分为(7,1)、(6,2)和(5,3)三组。根据题意,我们同时考虑使每行中的数和每列中数的和分别相等。 你能想出其他 11种填法吗? 例2 请你把 1-6这六个数字填在下面三角形的O内,使每条边上的数字之和相等。你能做到吗? 这是一种封闭型的数阵图,填写时的关键是确定三个顶点上的 数。1+2+3+4+5+6=21,用k表示每边上三个数的和,因为三个顶点上的数在求和时,都用了两次,用a,b,c表示三个顶点的数,使有21+a+b+c=3k因为a+b+c的最小值为6,最大值为15,所以3个k的最小值为27,最大为36,那么k的最小值是9,最大值是12。 ①当k=9时,a+b+c=6 这时 a=1,b=2,c=3; a=1,b=3,c=2; a=2,b=1,c=3; a=2,b=3,c=1; a=3,b=1,c=2; a=3,b=2,c=1; ②当k=10、11、12时,可仿照①的方法进行分析。 本题的填法有很多种,这里只列举其中的几种,其他的填法由同 学们自己考虑。 1、 将1,3,5,7,9 这五个数分别填入下图的各正方形中...