有限元分析第五章(第二部分)

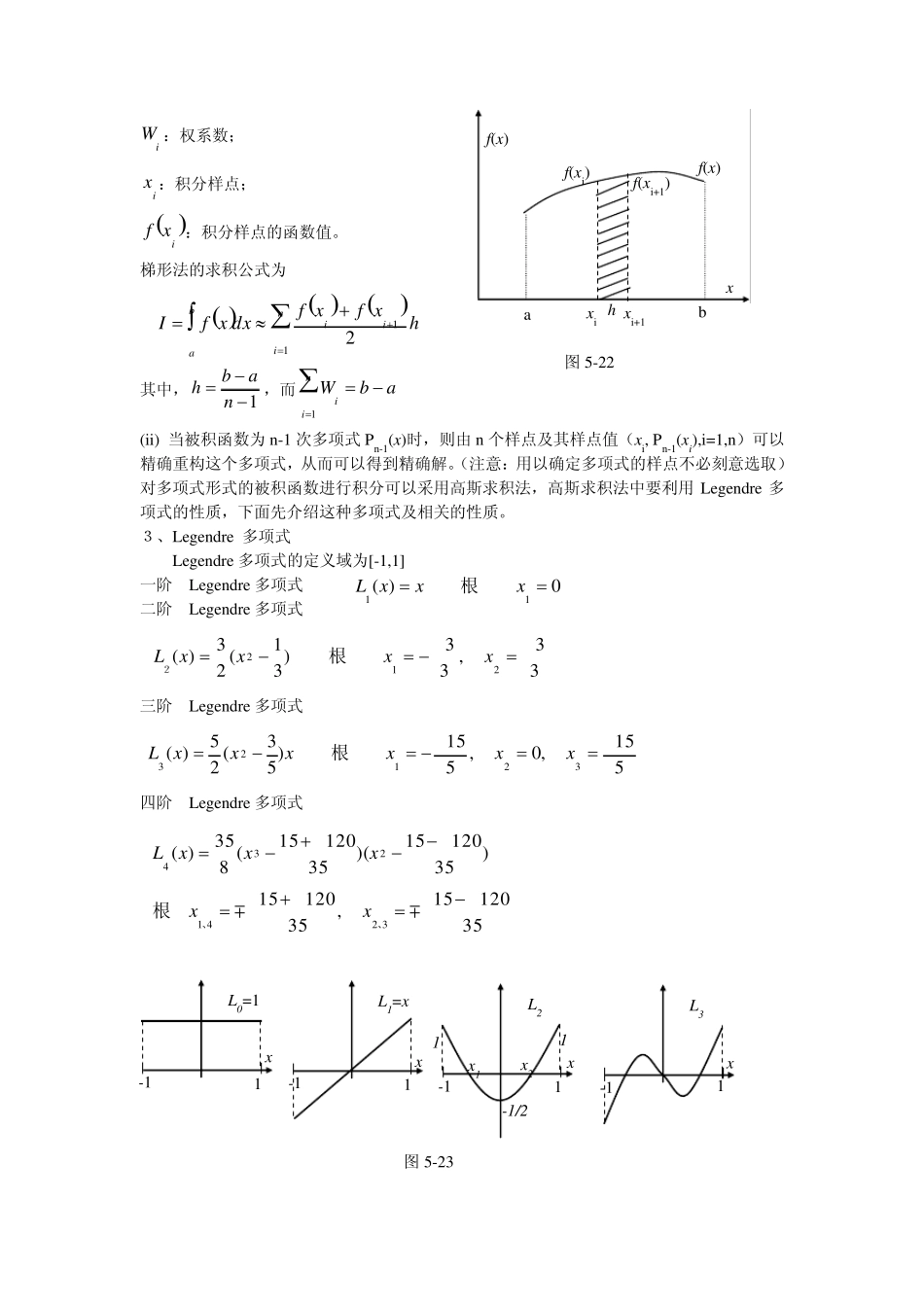
§ 5 -5 数值积分 １、问题的提出 在上一节中对等参元进行单元分析时要进行下列积分： (i) 单元刚度矩阵 (ii)体积力的等效结点力 (iii)边界力的等效结点力 (iv)温升载荷的等效结点力 式（5-4-5）~（5-4-8）分别归结为计算以下两种形式的积分 对于上述积分仅在单元的形状十分规则的情况下才能得到解析的结果（精确值），一般情况只能用数值积分方法（主要是高斯求积法）求近似值。虽然数值积分是“被迫“采用的，但后来发现：有选择地控制积分点的个数和位置，可以方便地实现我们的某些特殊意图。这样一来，数值积分就成为有限元分析的一个重要组成部分，以至本来可以精确积分的三角形单元也常常采用数值积分。 ２、数值积分的基本概念 任何积分工作取决于三个要素：给定的积分区间，给定的被积函数，具体的积分方法。下面以一维情况为例介绍数值积分的基本概念 (i) 梯形法 函数 xf在区间(a,b)的积分可以表达为   iniibaxfWdxxfI1  111111),()(dx dxyxfdxxf、          ddJtBEBtdx dyBEBkTTedet1111     ddJtffNtdffNryxTyxTeVdet1111      dJdtBTdet01111T      dyyfdxxftdsqpNrT1111,(5-4-5) (5-4-8) (5-4-7) (5-4-6) iW ：权系数； ix ：积分样点；  ixf：积分样点的函数值。 梯形法的求积公式为 其中， 1 nabh，而abWnii1 (ii) 当被积函数为n-1 次多项式Pn-1(x)时，则由n 个样点及其样点值（xi, Pn-1(xi),i=1,n）可以精确重构这个多项式，从而可以得到精确解。（注意：用以确定多项式的样点不必刻意选取）对多项式形式的被积函数进行积分可以采用高斯求积法，高斯求积法中要利用Legendre 多项式的性质，下面先介绍这种多项式及相关的性质。 ３、Legendre 多项式 Legendre 多项式的定义域为[-1,1] 一阶 Legendre 多项式 二阶 Legendre 多项式 三阶 Legendre 多项式 四阶 Legendre 多项式 0)(11xxxL 根 33,33)31(23)(212xxxxL 根 ２515,0,515)53(25)(32123xxxxxxL 根 3512015,3512015)3512015)(3512015(835)(3241234、、 根...