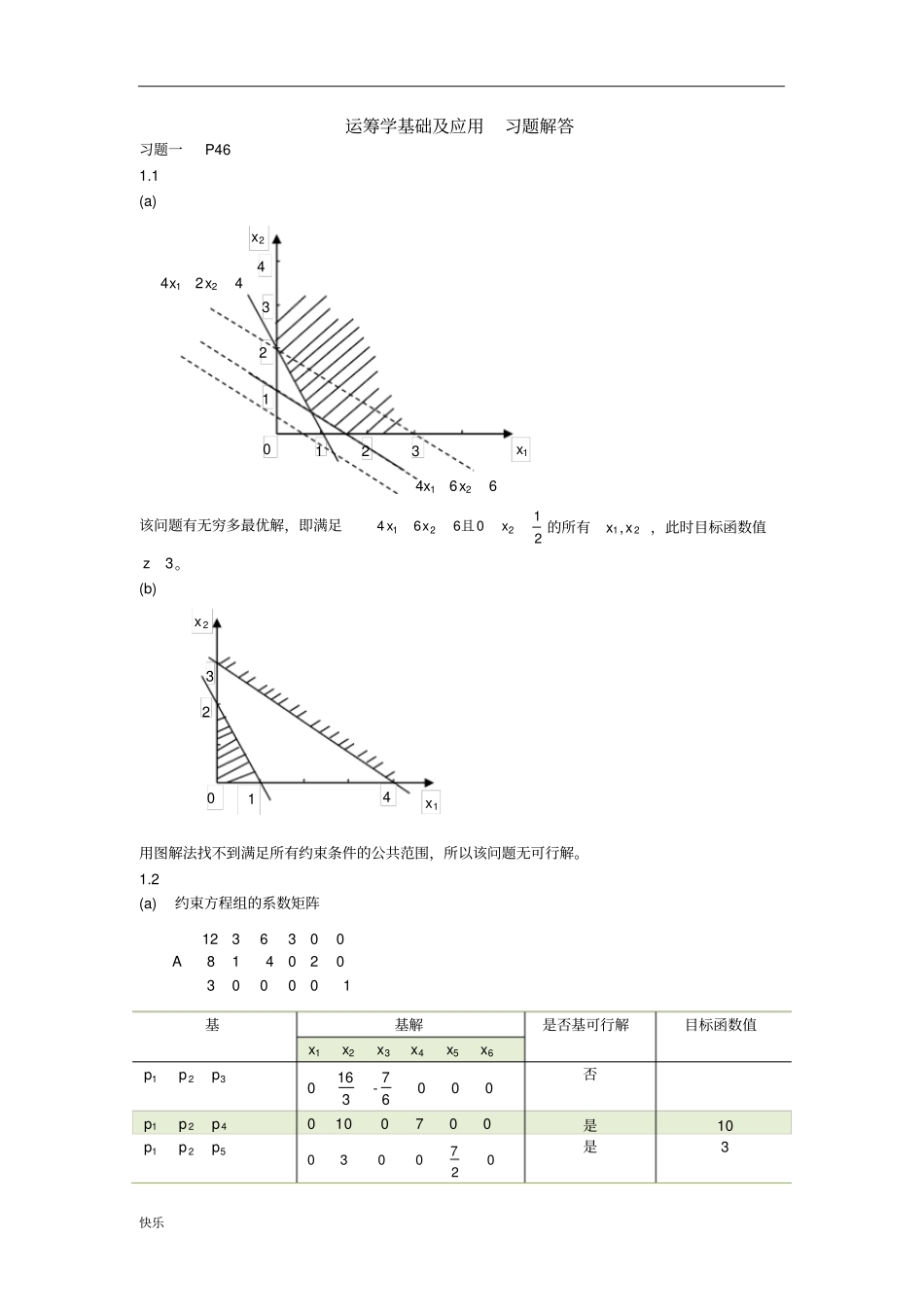
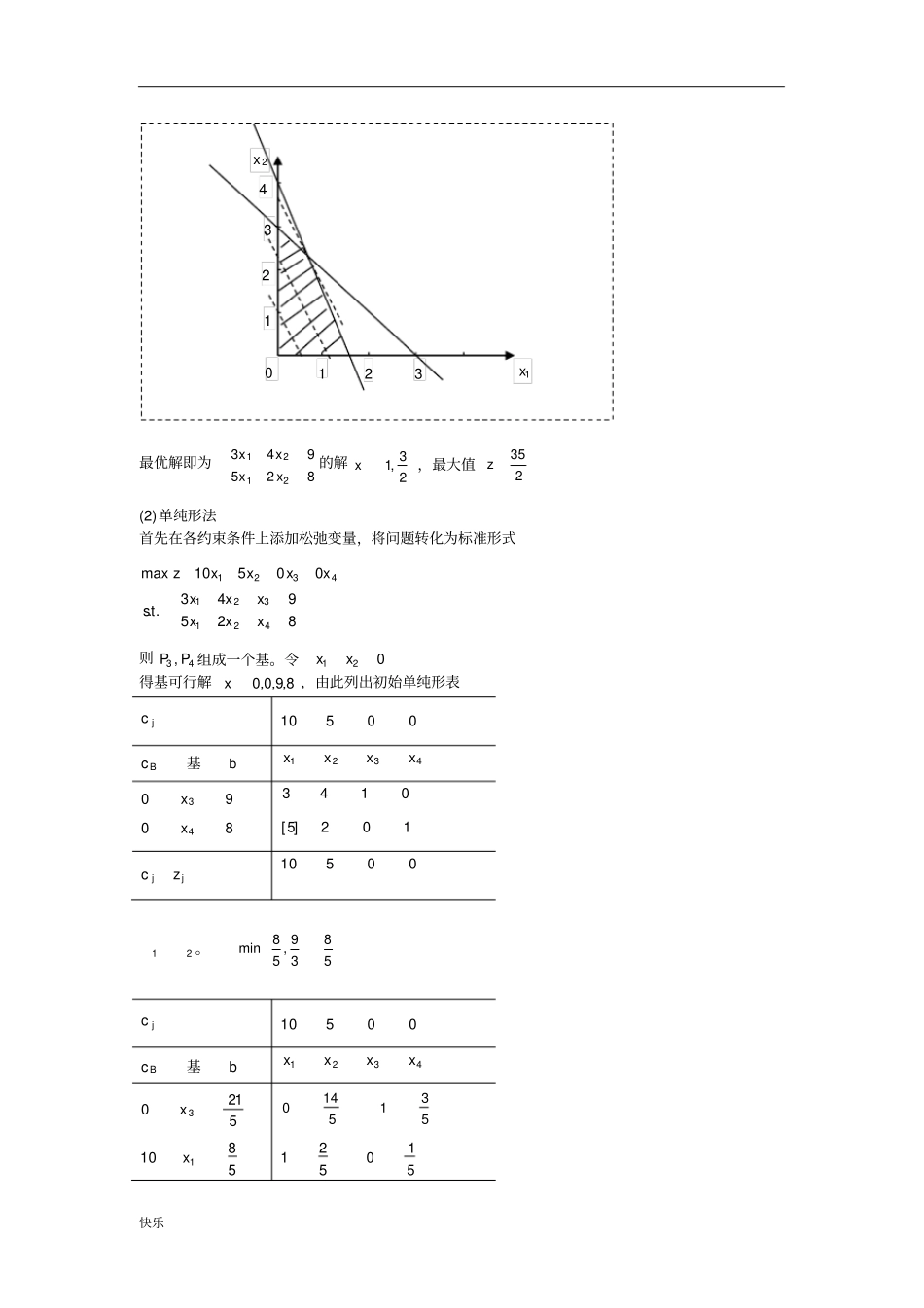
快乐运筹学基础及应用习题解答习题一P46 1.1 (a) 该问题有无穷多最优解,即满足210664221xxx且的所有21,xx,此时目标函数值3z。(b) 用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解。1.2 (a)约束方程组的系数矩阵1000030204180036312A基基解是否基可行解目标函数值654321xxxxxx321ppp00067-3160否421ppp0070010是10 521ppp0270030是3 0 1 4 2 3 2x1x0 2x1x1 2 3 4 1 3 2 66421xx42421xx快乐621ppp421000447否431ppp0082500否531ppp0802300是3 631ppp3002101否541ppp053000是0 641ppp415020045否最优解Tx0,0,7,0,10,0。(b) 约束方程组的系数矩阵21224321A基基解是否基可行解目标函数值4321xxxx21pp002114否31pp0511052是54341pp6110031否32pp02210是542pp20210否43pp1100是5最优解Tx0,511,0,52。1.3(a) (1) 图解法快乐最优解即为8259432121xxxx的解23,1x,最大值235z(2)单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式825943..00510max4213214321xxxxxxtsxxxxz则43 , PP组成一个基。令021xx得基可行解8,9,0,0x,由此列出初始单纯形表jc00501Bc基b4321xxxx903x0143804x102]5[jjzc0050121。5839,58minjc00501Bc基b4321xxxx51203x531514058101x5105210 2x1x1 2 3 4 1 3 2 快乐jjzc201002,2328,1421min新的单纯形表为jc00501Bc基b4321xxxx2352x143145101101x727101jjzc1425145000,21,表明已找到问题最优解0,0,231,4321xxxx。最大值235*z(b) (1) 图解法最优解即为524262121xxxx的解23,27x,最大值217z(2) 单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式1234523124125max2000515. . 62245zxxxxxxxstxxxxxx0 2x1x3 6 9 12 3 9 6 521xx242621xx快乐则3P ,4P ,5P 组成一个基。令021xx得基可行解0,0,15,24,5x,由此列出初始单纯形表jc2 1 0 0 0Bc基b1x2x3x4x5x0 3x15 0 4x24 0 5x5 0 5 1 0 0 [6] 2 0 1 0 1 1 0 0 1 jjzc2 1 0 0 021。24 5min,,461jc2 1 0 0 0Bc基b1x2x3x4x5x0 3x15 2 4x4 0 5x1 0 5 1 0 0 1 130 160 0 230 161 jjzc0 130 13002,1533min,24,522新的单纯形表为jc2 1 0 0 0Bc基b1x2x3x4x5x0 3x1520 0 1 54152快乐2 4x720 5x321 0 0 14120 1 0 1432jjzc0 0 0 14120,21,表明已找到问题最优解11x,272x,3152x,40x,50x。最大值*172z1.6 (a) 在 约 束 条...