运筹学胡运权版运输问题课后习题答案

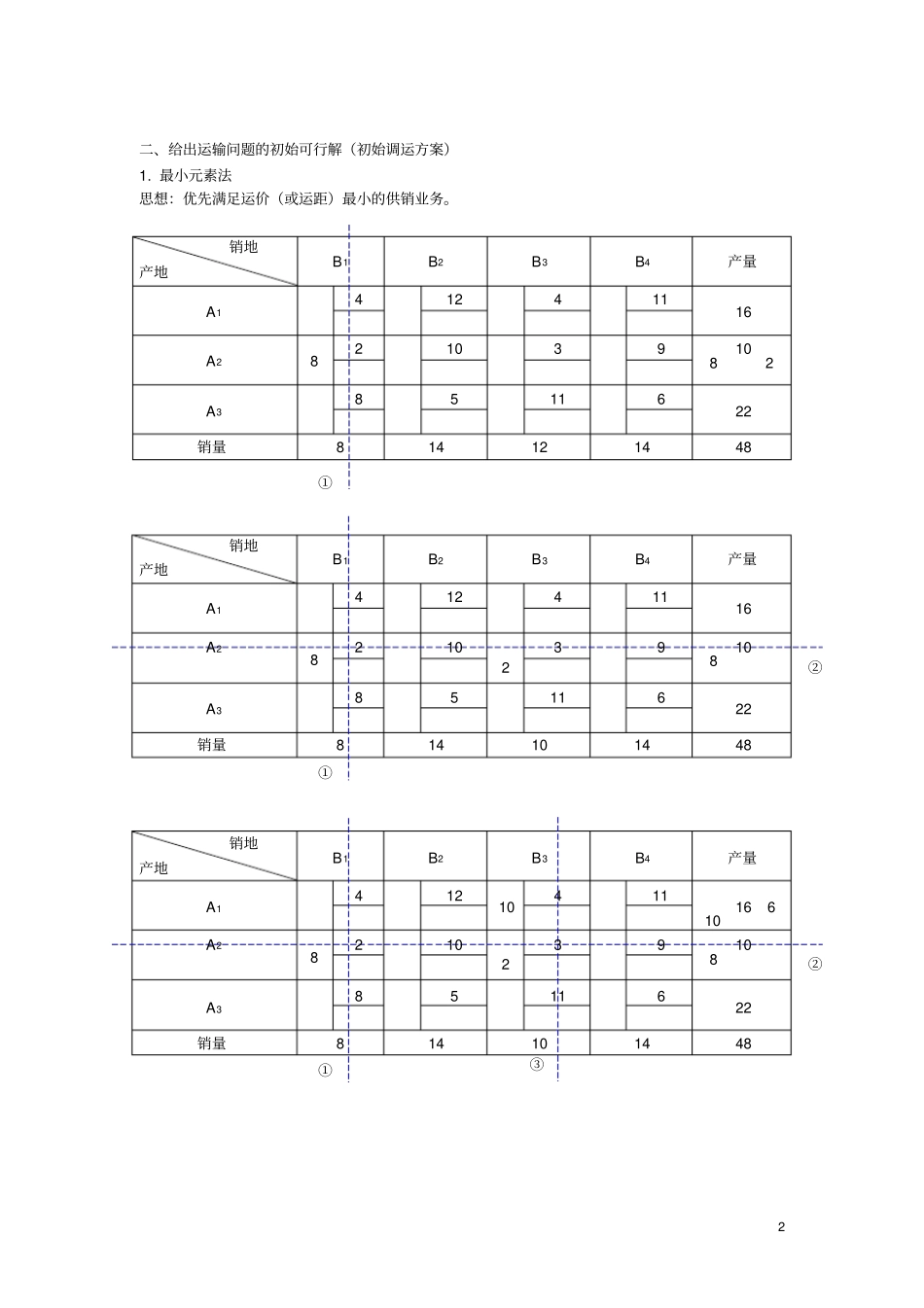
1 P66： 8.某部门有3 个生产同类产品的工厂（产地），生产的产品由4 个销售点出售，各工厂 A1， A2，A3 的生产量、各销售点B1，B2，B3，B4 的销售量（假定单位为t）以及各工厂到销售点的单位运价（元/t）示于下表中，问如何调运才能使总运费最小？表销地产地B1B2B3B4产量A14 12 4 11 16 A22 10 3 9 10 A38 5 11 6 22 销量8 14 12 14 48 解：一、该运输问题的数学模型为：可以证明：约束矩阵的秩为r (A) = 6. 从而基变量的个数为6. 34333231242322213141141312116115893102114124minxxxxxxxxxxxxxczijijij4,3,2,1;3,2,1,01412148221016342414332313322212312111343332312423222114131211jixxxxxxxxxxxxxxxxxxxxxxxxxij111213142122232431323334xxxxxxxxxxxx7 121111111111111111111111112 二、给出运输问题的初始可行解（初始调运方案）1. 最小元素法思想：优先满足运价（或运距）最小的供销业务。销地产地B1B2B3B4产量A14 12 4 11 16 A28 2 10 3 9 10 A38 5 11 6 22 销量8 14 12 14 48 销地产地B1B2B3B4产量A14 12 4 11 16 A28 2 10 3 9 10 A38 5 11 6 22 销量8 14 10 14 48 销地产地B1B2B3B4产量A14 12 10 4 11 16 6A28 2 10 3 9 10 A38 5 11 6 22 销量8 14 10 14 48 8 2 ①8 2 ②①8 2 ②①10 ③3 销地产地B1B2B3B4产量A14 12 10 4 11 16 6A28 2 10 3 9 10 A38 14 5 11 6 22 8销量8 14 10 14 48 销地产地B1B2B3B4产量A14 12 10 4 11 16 6A28 2 10 3 9 10 A38 14 5 11 8 6 22 0销量8 14 10 14 648 销地产地B1B2B3B4产量A14 12 10 4 6 11 16 0A28 2 10 3 9 10 0A38 14 5 11 8 6 22 0销量8 14 10 14 048 此时得到一个初始调运方案（初始可行解）：其余（非基） 变量全等于零。 此解满足所有约束条件，且基变量 （非零变量） 的个数为 6（等于 m+n-1=3+4-1=6). 总运费为（目标函数值）8 2 ②①10 ③14 ④8 2 ②①10 ③14 ④⑤8 2 ②①10 ③14 ④⑤⑥⑥,1013x,821x,223x,1432x,834x,614x3141ijijij xcZ4 2. 伏格尔（ Vogel)法伏格尔法的基本思想：运输表中各行各列的最小运价与次小运价之差值（罚数） 应尽可能地小。或者说： 优先供应罚数最大行（或列） 中最小运费的方格，以避免将运量分配到该行（或该列）次小运距的方格中。...