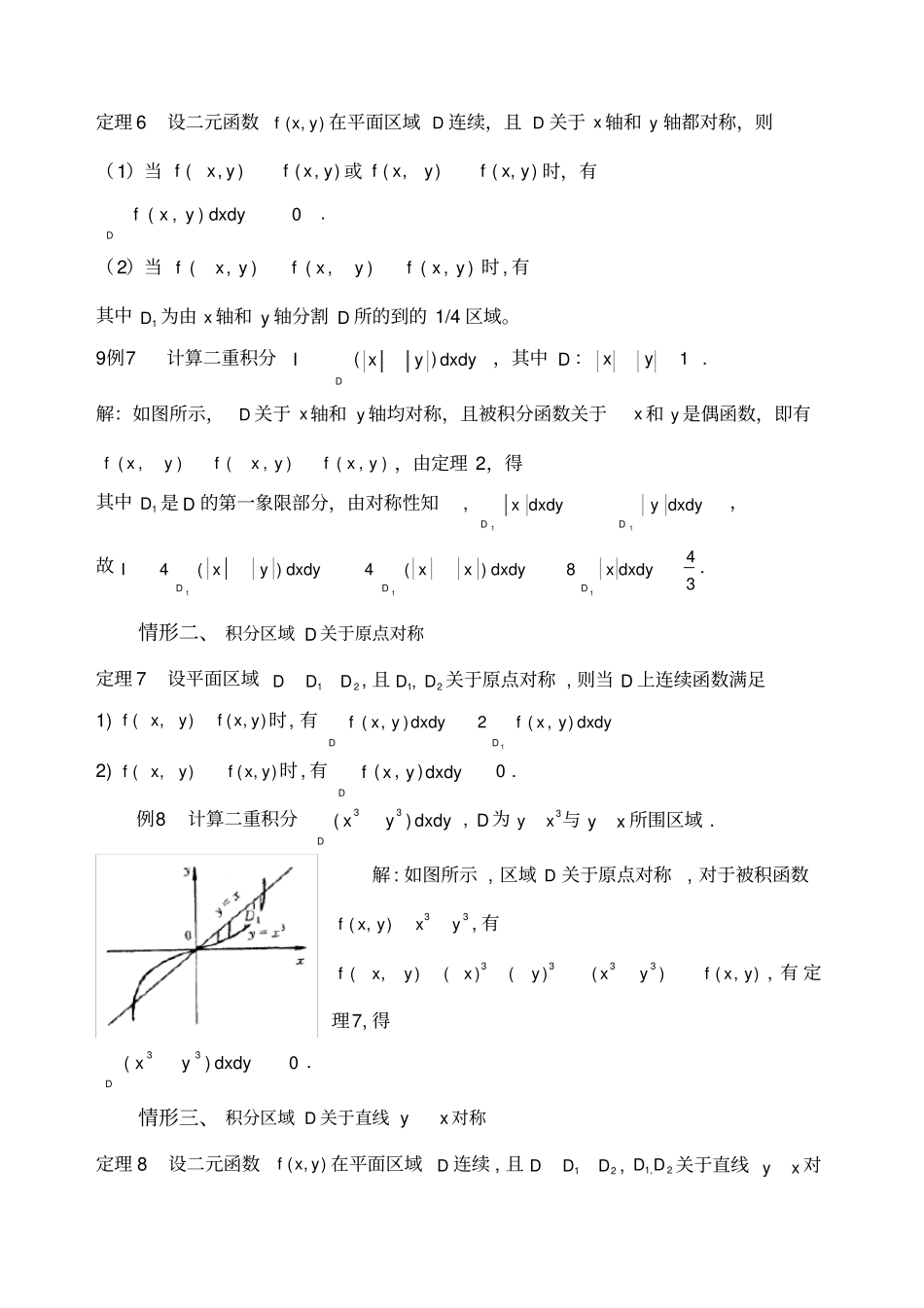
情形一: 积分区域 D 关于坐标轴对称定理 4设二元函数( ,)f x y 在平面区域 D 连续,且 D 关于 x 轴对称,则1) 当( ,)( , )f xyf x y (即( , )f x y 是关于 y 的奇函数)时,有(,)0Dfxy dxdy . 2) 当( ,)( , )f xyfx y (即( ,)fx y 是关于 y 的偶函数)时,有1(,)2(,)DDfxy dxdyfxy dxdy . 其中1D 是由 x 轴分割 D 所得到的一半区域。例 5 计算3()DIxyydxdy,其中 D 为由22yx 与2x围成的区域。解:如图所示,积分区域D 关于 x 轴对称 , 且3( ,)()( ,)fxyxyyfx y有即( ,)f x y 是关于 y 的奇函数,由定理13()0Dfxyydxdy. 类似地,有:定理 5设二元函数( ,)f x y 在平面区域 D 连续,且 D 关于 y 轴对称,则其中2D 是由 y 轴分割 D 所得到的一半区域。例6 计算2,DIx ydxdy其中D为由22;-220yxyxy及所围。解 : 如 图 所 示 ,D 关 于y 轴 对 称 , 并 且2(,)( ,)fx yx yfx y ,即被积分函数是关于x 轴的偶函数,由对称性定理结论有:11222220022215xDDIx ydxdyx ydxdydxxydxdy. 定理 6设二元函数( ,)f x y 在平面区域 D 连续,且 D 关于 x 轴和 y 轴都对称,则( 1)当(,)( ,)fx yfx y 或( ,)( ,)fxyfx y 时,有(,)0Dfxydxdy . ( 2)当(,)(,)(,)fxyfxyfxy时 , 有其中1D 为由 x 轴和 y 轴分割 D 所的到的 1/4 区域。9例7 计算二重积分()DIxydxdy,其中 D :1xy . 解:如图所示,D 关于 x轴和 y 轴均对称,且被积分函数关于x 和 y 是偶函数,即有(,)(,)(,)fxyfxyfxy,由定理 2,得其中1D 是 D 的第一象限部分,由对称性知,11DDx dxdyy dxdy,故14()DIxydxdy14()Dxxdxdy18Dx dxdy43. 情形二、 积分区域 D 关于原点对称定理 7 设平面区域12DDD , 且1,D2D 关于原点对称 , 则当 D 上连续函数满足1)(,)( ,)fxyf x y 时, 有1(,)2(,)DDfx y dxdyfxy dxdy2)(,)( ,)fxyf x y 时 , 有(,)0Dfxy dxdy. 例8 计算二重积分33()Dxydxdy , D 为3yx 与 yx 所围区域 . 解 : 如图所示 , 区域 D 关于原点对称, 对于被积函数33( ,)fx yxy , 有3333(,)()()()( ,)fxyxyxyfx y, 有 定理7, 得33()0Dxydxdy.情形三、 积分区域 D 关于直线 yx 对称定理 8 设二元函数( , )f x y 在平面区域D 连续 , 且12DDD ,1,2D D 关于...