第二章分离变量法VIP免费

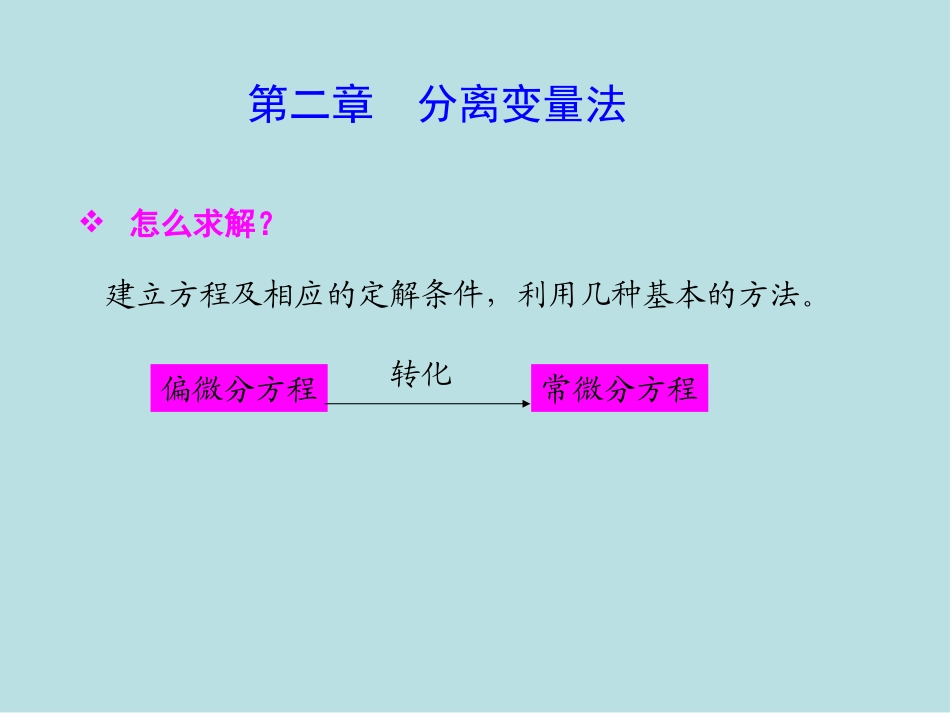
2222(,)uxtaut22,,,uaufxyztt),,()(zyxfu一、典型数理方程1、弦振动方程2、热传方程3、Laplace方程许多物理力学问题都可以归结为偏微分方程的定解问题。怎么求解？建立方程及相应的定解条件，利用几种基本的方法。偏微分方程常微分方程转化第二章分离变量法02xxttuau边界条件：)(0xut).(0xutt0),(0xtxu0),(lxtxu初始条件：（泛定方程）波动方程：A2.1有界弦的自由振动定解问题的特点：偏微分方程是线性齐次的，边界条件也是齐次的，求解此类问题可以采用叠加原理。定解问题的方法：找出偏微分方程满足边界条件的多个特解，再利用它们的线性组合，使满足初始条件。2468-1-0.50.510x固定lx自由345678-1-0.50.510x自由lx自由468-1-0.50.510x自由lx固定2.557.51012.515-1-0.50.510x固定lx固定对于确定的频率，振动过程中有不动的节点，这类振动波为驻波：振动过程中不动的点称为节点。振动过程中驻波的振幅达到最大值，称为腹点。为求定解问题，选择物理模型：乐器发出的声音可以分解为不同频率的单音，每种单音振动时为正弦曲线，其振幅不依赖时间(,)()sinuxtctx注：u(x,t)中含变量x的函数与含t的函数的乘积，有变量分离的形式波腹波节2.557.51012.515-1-0.50.51每一点绕平衡位置振动)(tT振幅随位置变化)(xX驻波解：)()(),(tTxXtxu将U=X(x)T(t)代入波动方程：0''''2TXaXT这是解的分离变量0)()0(tTX0)()(tTlX0)0(X和0)(lX2''''TXaTX0''''2TXaXT将U=X(x)T(t)代入边界条件：和T(t)为任意值，要使上式成立，则：)()('')()(''2xXxXtTatTClearlyx,t是相互独立的变量，这个方程的两边互不统属，而各自独立变化。故比值只能为一常数！)()('')()(''2xXxXtTatT由分离变量，波动方程（偏微分方程）变为常微分方程组：;0''2TaT;0''XX0)0(X和.0)(lX(1)00''XXxxeCeCxX21)(0)0(X021CC(A).;0''XX的解：;0''XX0)0(X和.0)(lX对于某些值，方程的解存在，则称的值为固有值。相应的X(x)的解为固有函数。对于分三种情况加以讨论：()0Xl021lleCeC021CC0Xx(2)021)(CxCxX02C021CC0)0(X()0Xl0Xx(3)0xCxCxXsincos)(210)0(X01C.0)(lX0sin2lC2()sinnnxXxCl222ln：固有值lxnCxXsin)(2：特征函数(固有函数);0''XX本征值方程C2是积分常数222ln3,2,1n0sin2lC对于方程，因为X(x)不恒等于零。0sinl02C只有超越方程B.;0''2222TlanT()cossin,nnatnatTtABllA、B是积分常数。(,)(cossin)sinnnnnatnatnxuxtABlll3,2,1n222ln：固有值代入T的方程;0''2TaT;0''XX0)0(X和.0)(lXAn=A*C2是积分常数合并,线性齐次，可采用叠加原理1(,)(cossin)sin.nnnnatnatnxuxtABlllC.)(0xut由初始条件：),(sin1xlxnAnn;sin)(20dlnlAln0()ttux).(sin1xlxnBlannn.sin)(20dlnanBlnFourier展开式的系数：Fourier展开式的系数：小结分离变量：)()(),(tTxXtxu0''''2TXaXT0)()0(tTX0)()(tTlX.sin)sincos(),(1lxnlatnBlatnAtxunnn边值确定本征值函数：.sin)sincos(),(lxnlatnBlatnAtxunnn初值确定叠加系数：;sin)(20dlnlAln.sin)(20dlnanBln注意：边界值等于零（齐次边界条件）是确定本征函数的根本。（二）例例1磁致伸缩换能器－两端自由的均匀细杆。自由：振动传递给外界0lxA.)()(),(tTxXtxu0''''2TXaXT0)()0('tTX0)()('tTlX分离变量：;0''2TaT;0''XX0)0('X和.0)('lXxCxCxXsincos)(21B.,02C0)cossin(21lClC222ln3,2,1,0n02xxttuau0),(lxxtxu0),(lxxtxu)(0xut)()(0xxuttlxnCxXcos)(1C.;0''2222Tla...