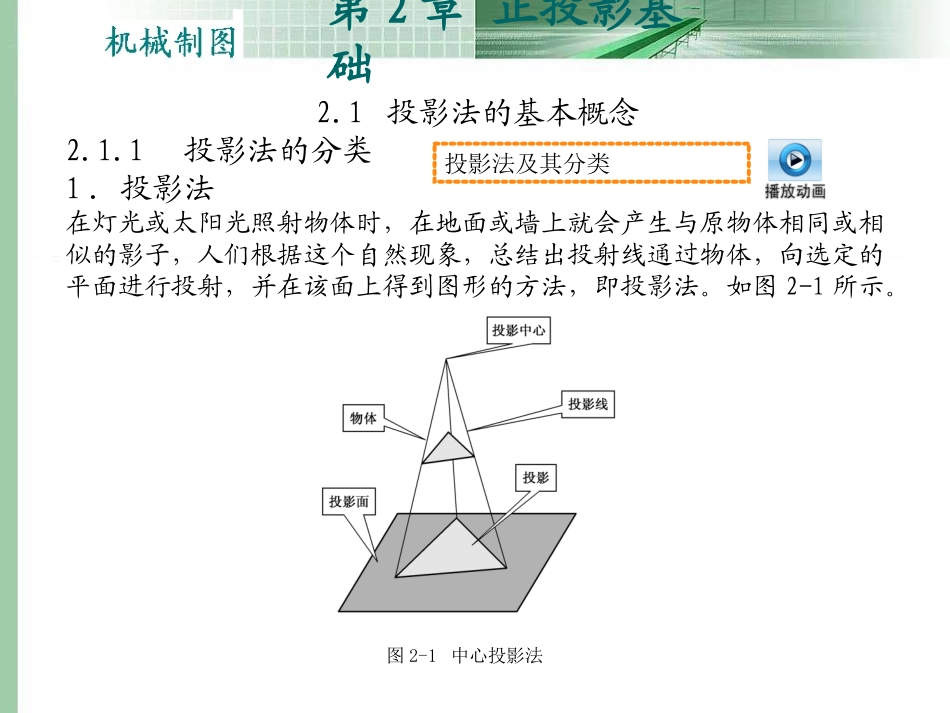
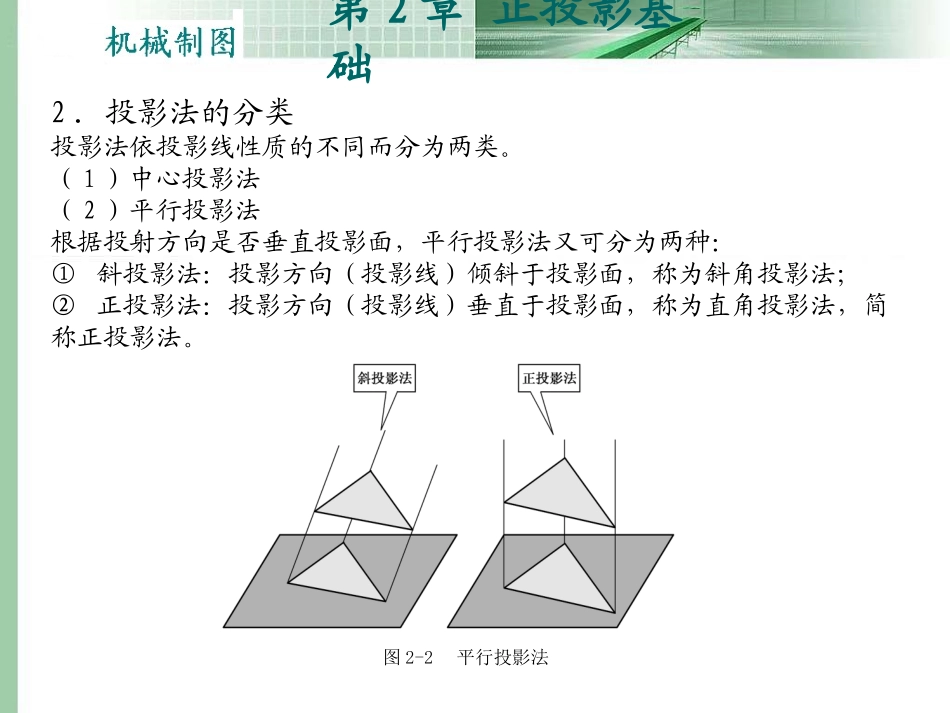
第2章正投影基础2.1投影法的基本概念2.2三视图及其对应关系2.3点的投影2.4直线的投影2.5平面的投影2.6基本几何体的投影2.7几何体的尺寸注法2.8几何体的轴测图第2章正投影基础2.1投影法的基本概念2.1.1投影法的分类1.投影法在灯光或太阳光照射物体时,在地面或墙上就会产生与原物体相同或相似的影子,人们根据这个自然现象,总结出投射线通过物体,向选定的平面进行投射,并在该面上得到图形的方法,即投影法。如图2-1所示。图2-1中心投影法投影法及其分类第2章正投影基础2.投影法的分类投影法依投影线性质的不同而分为两类。(1)中心投影法(2)平行投影法根据投射方向是否垂直投影面,平行投影法又可分为两种:①斜投影法:投影方向(投影线)倾斜于投影面,称为斜角投影法;②正投影法:投影方向(投影线)垂直于投影面,称为直角投影法,简称正投影法。图2-2平行投影法第2章正投影基础3.投影的基本特性(1)中心投影法投射中心、物体、投影面三者之间的相对距离对投影的大小有影响。物体位置改变,投影大小也改变。度量性较差。如图2-3所示。(2)平行投影法投影大小与物体和投影面之间的距离无关。度量性较好。如图2-2所示。图2-3中心投影法特性第2章正投影基础2.1.2正投影的基本特性1.真实性2.积聚性3.类似性图2-4直线段、平面形的正投影特性正投影的基本特性第2章正投影基础2.2三视图及其对应关系2.2.1三视图的形成过程1.三个投影面的建立物体具有三个方向尺寸和上下、前后、左右方向的形状,因此,一面视图不能表示物体的全貌,所以需采用多面投影来表示物体形状。一般需将物体放置在如图2-6所示的用互相垂直3个投影面组成的三面投影体系中,分别向三个投影面进行投影,然后将所得到的三个投影联系起来,互相补充即可反映出物体的真实形状和大小。2.三投影面名称正立投影面—正立着的面,简称正投影面或V面;水平投影面—水平的面为水平投影面,简称水平面或H面;侧立投影面—侧立着的面为侧投影面,简称侧面或W面。在三投影面中:OX轴—V面和H面的交线;OY轴—H面和W面的交线;OZ轴—V面和W面的交线;坐标原点—OX、OY、OZ三轴的交点。3.三视图的形成三视图的生成原理第2章正投影基础图2-6三面投影体系图2-7三视图的形成图2-8三视图的展开过程第2章正投影基础值得注意的是,在生产中不需要画出投影轴和表示投影面的边框,视图按上述位置布置时,不需注出视图名称,如图2-9所示。图2-9三视图第2章正投影基础2.2.2三视图之间的对应关系从三视图的形成过程和投影面展开的方法中,可明确以下关系。1.位置关系俯视图在主视图的下边,左视图在主视图的右边,如图2-10所示。图2-10三视图的位置关系三视图的投影规律第2章正投影基础2.方位关系任何物体都有上下、前后、左右六个方位。而每个视图只能表示其4个方位,如图2-11所示。图2-11三视图的方位关系第2章正投影基础3.三等关系任何物体都有长、宽、高3个尺寸,如图2-12所示。若将物体左右方向(X方向)的尺度称为长,上下方向(Z方向)尺度称为高,前后方向(Y方向)尺度称为宽,则在三视图上主、俯视图反映了物体的长度;主、左视图反映了物体的高度;俯、左视图反映了物体的宽度。图2-12三视图的三等关系第2章正投影基础2.3点的投影2.3.1点的三面投影1.点在一个投影面上的投影2.点的三面投影图2-13点在一个投影面上的投影图2-14一条投射线上的多个点在一个投影面上的投影第2章正投影基础根据工程图样的需要,需把点放置在三面投影体系中进行投影,这时点的位置是确定的,如图2-15所示。图2-15点的三面投影第2章正投影基础2.3.2点的投影与直角坐标1.空间点A在3个投影面上的投影2.投影面的展开如图2-16所示,将三投影面展开,使其与V面成同一平面。图2-16点的三面投影展开方法第2章正投影基础3.点的投影规律按照点与三投影面关系,由立体展开成平面,可得出点的三面投影规律。(1)点的正面投影和水平投影的连线垂直于X轴,两投影都反映横坐标,表示空间点到侧投影面的距离。即:aa⊥OX轴。(2)点的正面投影a和侧面投影a的连线垂直于Z轴,这两个投影都反映空间点的Z坐标,即表示点到水平投影面的距离...