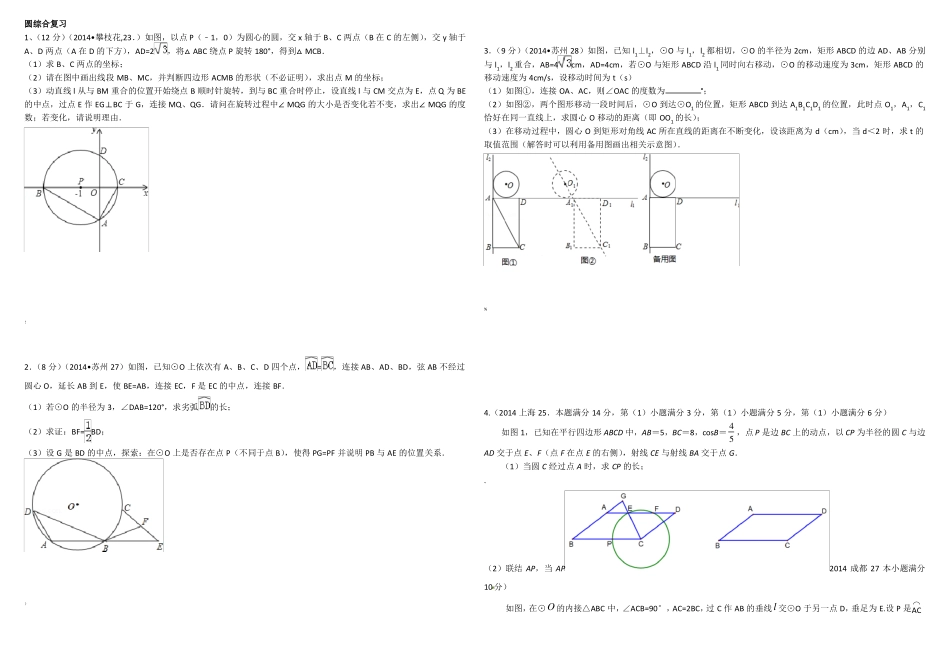
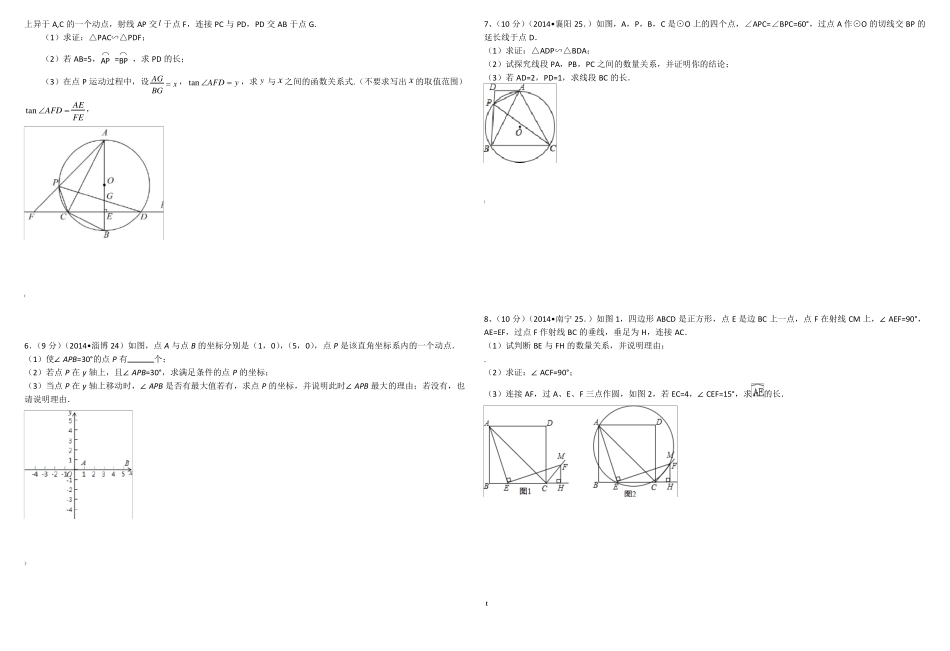
圆综合复习1、(12 分)(2014•攀枝花,23.)如图,以点 P(﹣1,0)为圆心的圆,交 x 轴于 B、C 两点(B 在 C 的左侧),交 y 轴于A、D 两点(A 在 D 的下方),AD=2,将△ ABC 绕点 P 旋转 180°,得到△ MCB.(1)求 B、C 两点的坐标;(2)请在图中画出线段 MB、MC,并判断四边形 ACMB 的形状(不必证明),求出点 M 的坐标;(3)动直线 l 从与 BM 重合的位置开始绕点 B 顺时针旋转,到与 BC 重合时停止,设直线 l 与 CM 交点为 E,点 Q 为 BE的中点,过点 E 作 EG⊥BC 于 G,连接 MQ、QG.请问在旋转过程中∠ MQG 的大小是否变化若不变,求出∠ MQG 的度数;若变化,请说明理由.!2.(8 分)(2014•苏州 27)如图,已知⊙O 上依次有 A、B、C、D 四个点,=,连接 AB、AD、BD,弦 AB 不经过圆心 O,延长 AB 到 E,使 BE=AB,连接 EC,F 是 EC 的中点,连接 BF.(1)若⊙O 的半径为 3,∠DAB=120°,求劣弧的长;(2)求证:BF= BD;(3)设 G 是 BD 的中点,探索:在⊙O 上是否存在点 P(不同于点 B),使得 PG=PF 并说明 PB 与 AE 的位置关系.)3.(9 分)(2014•苏州 28)如图,已知 l1⊥l2,⊙O 与 l1,l2 都相切,⊙O 的半径为 2cm,矩形 ABCD 的边 AD、AB 分别与 l1,l2 重合,AB=4cm,AD=4cm,若⊙O 与矩形 ABCD 沿 l1 同时向右移动,⊙O 的移动速度为 3cm,矩形 ABCD 的移动速度为 4cm/s,设移动时间为 t(s)(1)如图①,连接 OA、AC,则∠OAC 的度数为°;(2)如图②,两个图形移动一段时间后,⊙O 到达⊙O1 的位置,矩形 ABCD 到达 A1B1C1D1 的位置,此时点 O1,A1,C1恰好在同一直线上,求圆心 O 移动的距离(即 OO1 的长);(3)在移动过程中,圆心 O 到矩形对角线 AC 所在直线的距离在不断变化,设该距离为 d(cm),当 d<2 时,求 t 的取值范围(解答时可以利用备用图画出相关示意图).%4.(2014 上海 25.本题满分 14 分,第(1)小题满分 3 分,第(1)小题满分 5 分,第(1)小题满分 6 分)如图 1,已知在平行四边形 ABCD 中,AB=5,BC=8,cosB= 45 ,点 P 是边 BC 上的动点,以 CP 为半径的圆 C 与边AD 交于点 E、F(点 F 在点 E 的右侧),射线 CE 与射线 BA 交于点 G.(1)当圆 C 经过点 A 时,求 CP 的长;~(2)...