二元线性回归模型案例

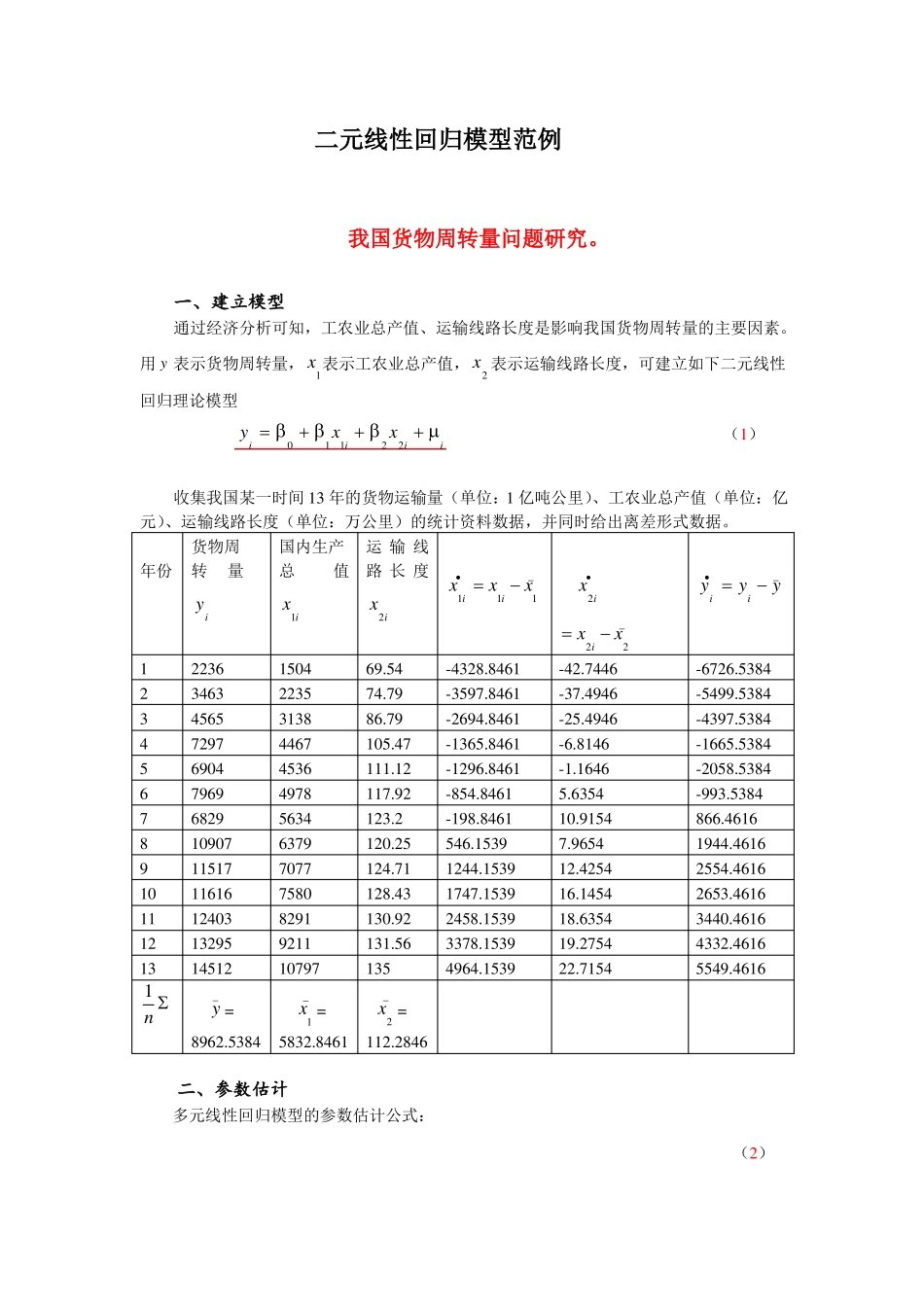
二元线性回归模型范例我国货物周转量问题研究。一、建立模型通过经济分析可知，工农业总产值、运输线路长度是影响我国货物周转量的主要因素。用 y 表示货物周转量， x1表示工农业总产值， x2 表示运输线路长度，可建立如下二元线性回归理论模型收集我国某一时间 13 年的货物运输量（单位：1 亿吨公里）、工农业总产值（单位：亿元）、运输线路长度（单位：万公里）的统计资料数据，并同时给出离差形式数据。货物周国内生产运 输 线年份转量总值路 长 度•_yi  0  1x1i  2x2i  i（1）•yi123456789101112132236346345657297690479696829109071151711616124031329514512x1i15042235313844674536497856346379707775808291921110797x1 =x2i69.5474.7986.79105.47111.12117.92123.2120.25124.71128.43130.92131.56135x2 =x1i  x1i  x1x2i x2i  x2_yi  yi  y•_-4328.8461-3597.8461-2694.8461-1365.8461-1296.8461-854.8461-198.8461546.15391244.15391747.15392458.15393378.15394964.1539-42.7446-37.4946-25.4946-6.8146-1.16465.635410.91547.965412.425416.145418.635419.275422.7154-6726.5384-5499.5384-4397.5384-1665.5384-2058.5384-993.5384866.46161944.46162554.46162653.46163440.46164332.46165549.46161y =n8962.53845832.8461112.2846二、参数估计多元线性回归模型的参数估计公式：（2）eeei（3）ˆ =n  k 1n  k 122ˆ )   2 (XX)1（4）Cov(eiee= cii=cii（5）2n  k 1n  k 1其中，c1ii 为(XX)主对角线上元素。sVar( i ) =c e 2iiiin  k 1对于二元线性回归模型，由正规方程组可以得到参数估计公式如下••• 2••••( x1i yi )( x 2i )  ( x2i yi )( x1i x2i )1 ( x• 2• 21i )( x 2i )  ( x••21i x2i )••• 2••••( x2i yi)( x1i)  ( x1i yi)( x1i x2i)2 ( x• 2• 2••1i)( x2i)  ( x21i x2i)0  y 1 x1 2 x2由于 1 n00(XX)1k 2 =  0 x•22i x•• 1i x2i LL x•1i x•2i x• 21i0LL其中2x)( x•2•L  (•1ix•22i ) ( x1...