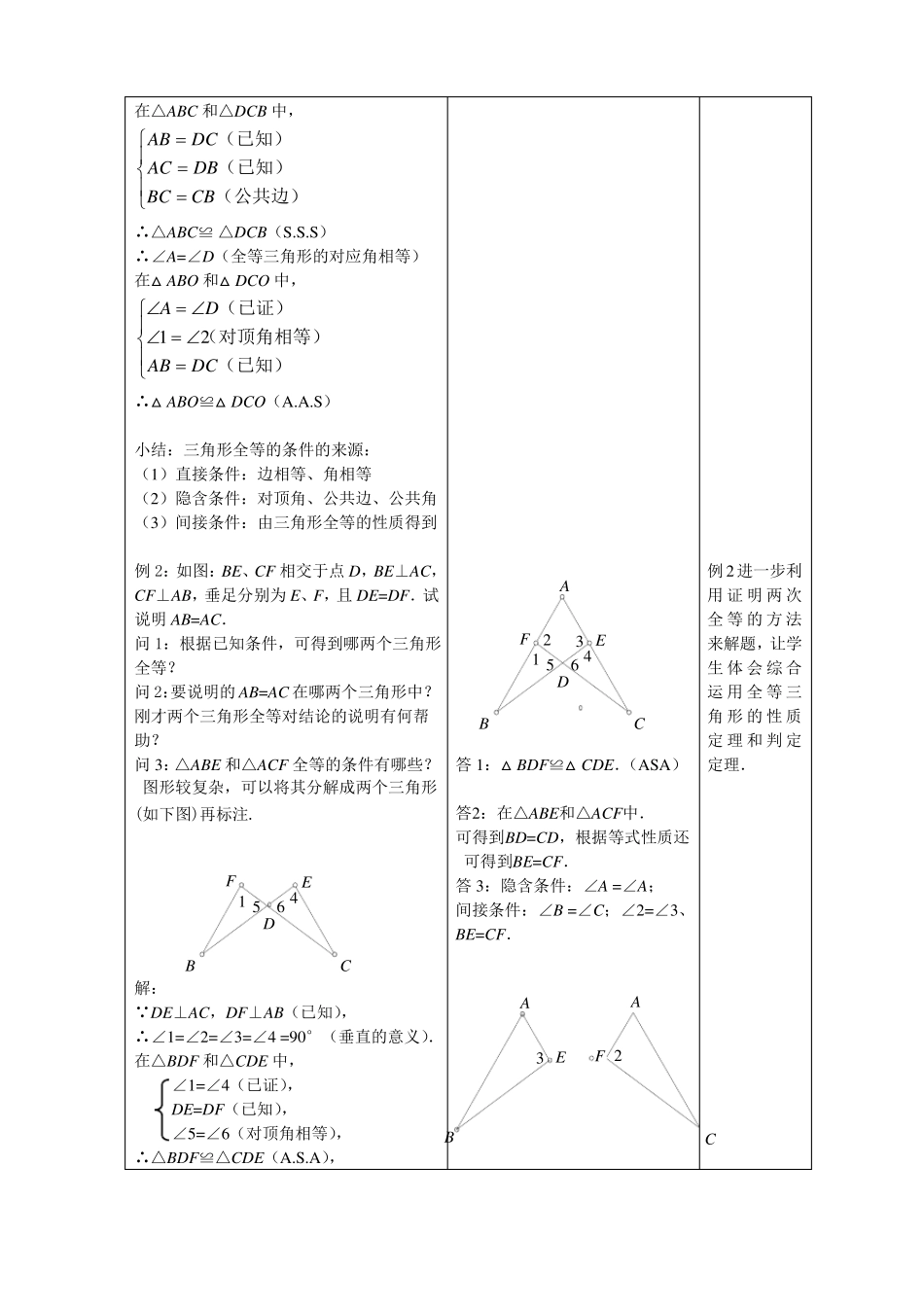
§14.4 全等三角形的判定(6)教学目标:1.经历添条件判定三角形全等的探索过程,复习三角形全等的判定方法.2.综合运用全等三角形性质和判定定理,解决简单的边角相等问题.教学重点及难点:利用两次全等的方法解决简单的几何问题.教学过程:教师活动一、复习引人:思考:如图,已知△ABC 和△DCB 中,AB=DC,请 补 充 一 个 条 件 能 直 接 判 定 △ABC≌△DCB,这个条件是.问 1:判定两个全等三角形的方法有哪些?问 2:要说明△ABC 和△DCB 全等,已知什么?还需添加什么条件?二、新课师:在上题中,△ ABO 和△ DOC 全等吗?例 1:如图,已知△ ABC 和△DCB 中,AB=DC,(AC=DB),试说明 △ ABO 和△ DCO 全等的理由.由△ABC≌ △DCB.(已证)问 1:这两个三角形全等对说明△ ABO 和△ DCO 全等有什么帮助?问 2:△ ABO 和△ DCO 全等的条件有哪些?图形较复杂,可以将其分解(如下图)再标注.BA学生活动ADOCB答 1:判定一般三角形全等有四种方法:S.A.S;A.S.A;A.A.S;S.S.S.答 2:从边上看;已知 两边→找 第三边AC=DB(S.S.S)从角上看::已知两边→找夹角∠ ABC=∠DCB (S.A.S)ADO12CB设计意图通过思考,复习 全 等 三 角形 的 判 定 定理,能在已知条 件 的 基 础上,根据全等三 角 形 的 判定定理,填上适当的条件,使 得 三 角 形全等.例 1 是在思考的基础上,让学 生 初 步 感知 可 以 利 用证 出 第 一 对三角形全等,答:可得到∠A=∠D.再 运 用 全 等三 角 形 性 质答 3:直接条件:AB=DC;得 出 说 明 第隐含条件:∠1=∠2;二 对 三 角 形间接条件:∠A=∠D.全等的条件.DADO12CCBC B解:在△ABC 和△DCB 中,AB DC(已知)AC DB(已知)BC CB(公共边)∴△ABC≌ △DCB(S.S.S)∴∠A=∠D(全等三角形的对应角相等)在△ ABO 和△ DCO 中,A D(已证)21 (对顶角相等)AB DC(已知)∴△ ABO≌△ DCO(A.A.S)小结:三角形全等的条件的来源:(1)直接条件:边相等、角相等(2)隐含条件:对顶角、公共边、公共角(3)间接条件:由三角形全等的性质得到例 2:如图:BE、CF 相交于点 D,BE⊥AC,CF⊥AB,垂足分别为 E、F,且 DE=DF.试说明 AB=AC.问 1:根据已知条件,可得到哪两个三角形全等?问 2:要说明的 AB=AC 在哪两个...