理论力学谢传锋第九章习题解答

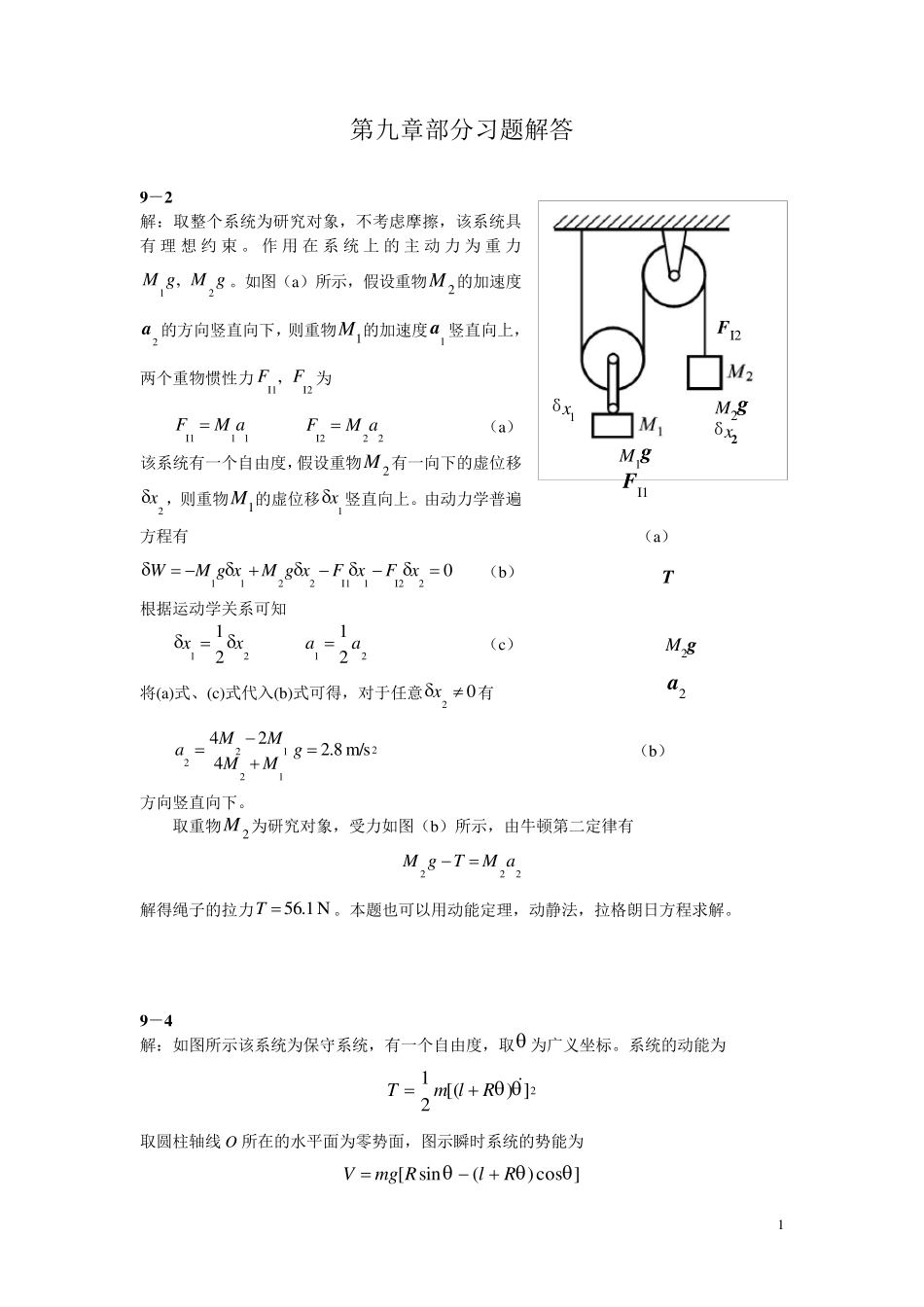
1 第九章部分习题解答 9 －2 解：取整个系统为研究对象，不考虑摩擦，该系统具有理想约束。作用在系统上的主动力为重力gMgM21 ,。如图（a）所示，假设重物2M 的加速度2a 的方向竖直向下，则重物1M 的加速度1a 竖直向上，两个重物惯性力I2I1, FF为 11I1aMF  22I2aMF  （a） 该系统有一个自由度，假设重物2M 有一向下的虚位移2x，则重物1M 的虚位移1x竖直向上。由动力学普遍方程有 （a） 02I21I12211xFxFxgMxgMW （b） 根据运动学关系可知 2121 xx 2121 aa  （c） 将(a)式、(c)式代入(b)式可得，对于任意02 x有 212122m/s8.2424gMMMMa （b） 方向竖直向下。 取重物2M 为研究对象，受力如图（b）所示，由牛顿第二定律有 222aMTgM 解得绳子的拉力N1.56T。本题也可以用动能定理，动静法，拉格朗日方程求解。 9 －4 解：如图所示该系统为保守系统，有一个自由度，取 为广义坐标。系统的动能为 2])[(21 RlmT 取圆柱轴线O 所在的水平面为零势面，图示瞬时系统的势能为 ]cos)(sin[RlRmgV M1g M2g FI2 FI1 δx2 δx1 M2g T a2 2 拉格朗日函数VTL，代入拉格朗日方程 0)(LLdtd 整理得摆的运动微分方程为 0sin)(2gRRl。 9 －6 解：如图所示，该系统为保守系统，有一个自由度，取弧坐标s 为广义坐标。系统的动能为 221SmT 取轨线最低点 O 所在的水平面为零势面，图示瞬时系统的势能为 mghV  由题可知bsdsdh4sin，因此有bsdbshSo8s42 。则拉格朗日函数 22821sbmgsmVTL 代入拉格朗日方程0)(sLsLdtd，整理得摆的运动微分方程为04sbgs。解得质点的运动规律为)21sin(0tbgAs，其中0, A为积分常数。 9 －1 3 解：1.求质点的运动微分方程 圆环（质量不计）以匀角速度 绕铅垂轴 AB 转动，该系统有一个自由度，取角度 为广义坐标。系统的动能为 22)sin(21)(21rmrmT 如图所示，取0为零势位，图示瞬时系统的势能为 零势面 h 零势面 3 )cos1( mgrV 则拉格朗日函数 )cos1()sin(212222mgrmrVTL 代入拉格朗日方程0)(LLdtd，整理得质点的运动微分方程为 0sin)cos(2rg 2.求维持圆环作匀速转动...