瓦尔拉斯均衡证明

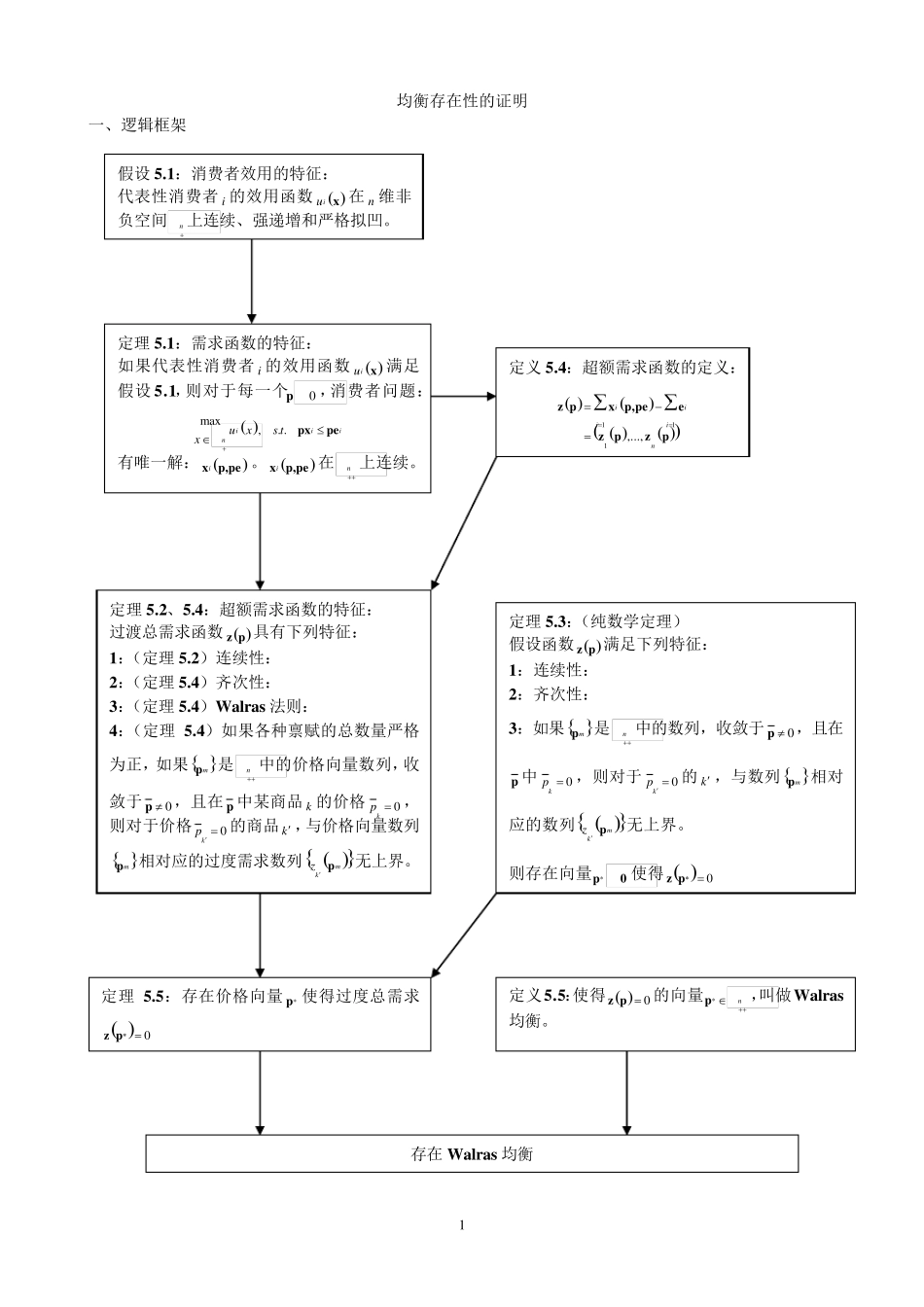
1 均衡存在性的证明 一、 逻辑框架 假设 5.1：消费者效用的特征： 代表性消费者 i 的效用函数 iux 在n 维非负空间n 上连续、强递增和严格拟凹。 定理 5.1：需求函数的特征： 如果代表性消费者 i 的效用函数 iux 满足假设 5.1，则对于每一个0p，消费者问题：  max,. .iiin uxs txpxpe 有唯一解：ix p,pe 。ix p,pe 在n 上连续。 定义 5.4：超额需求函数的定义：    111,...,nniiiinz px p,peez pzp 定理 5.2、5.4：超额需求函数的特征： 过渡总需求函数  z p 具有下列特征： 1：（定理 5.2）连续性： 2：（定理 5.4）齐次性： 3：（定理 5.4）Walras 法则： 4：（定理 5.4）如果各种禀赋的总数量严格为正，如果 mp是n 中的价格向量数列，收敛于0p，且在p 中某商品 k 的价格0kp  ，则对于价格0kp 的商品 k，与价格向量数列 mp相对应的过度需求数列 mkz p无上界。 定理 5.3：（纯数学定理） 假设函数  z p 满足下列特征： 1：连续性： 2：齐次性： 3：如果 mp是n 中的数列，收敛于0p，且在p 中0kp  ，则对于0kp 的k，与数列 mp相对应的数列 mkz p无上界。 则存在向量*p0 使得   0*z p 定理 5.5：存在价格向量*p 使得过度总需求  0*z p 定义5.5：使得  0z p的向量*np，叫做Walras均衡。 存在Walras 均衡 2 证明定理5.4（3）：如果每个消费者的效用函数都满足假设5.1，并且各种禀赋的总数量严格为正，10Iiie，如果 mp 是n 中的价格向量数列，收敛于0p，且在p 中某些商品k 的价格0kp  ，则对于价格0kp 的商品k ，与价格向量数列 mp相对应的总超额需求数列 mkz p无上界。 含义：如果一些而非所有商品的价格任意接近于0，那么那些商品至少有一种的超额需求将会无限高 解释： 1.  mp定义在n 中，即对于所有的m ，有0mp。 2. 当 m   ，m pp ，p 的特征为0p且0p；同时，由于在p中某些坐标为零，0kp ，所以，p 并不严格大于零向量，如，1211,,...,,0 ,,...,kknp ppppp。也就是说，当 m   时，m pp ，0mk p。 3. p 中为零的坐标，第 k 个坐标，...